Challenge Exploration
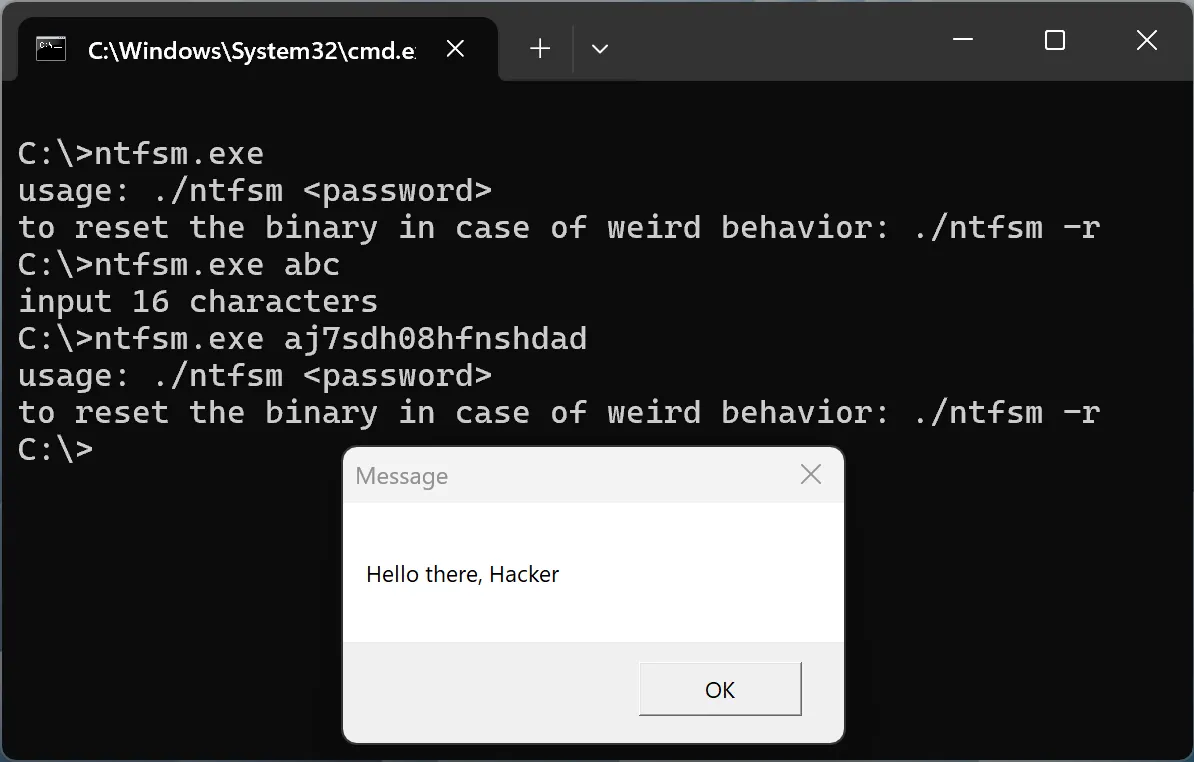
The challenge gives us a Windows executable file called ntfsm.exe, which asks for a 16-character password as an argument. I tried with a random 16-character password and it yielded a message box.
Doing The Disassembling
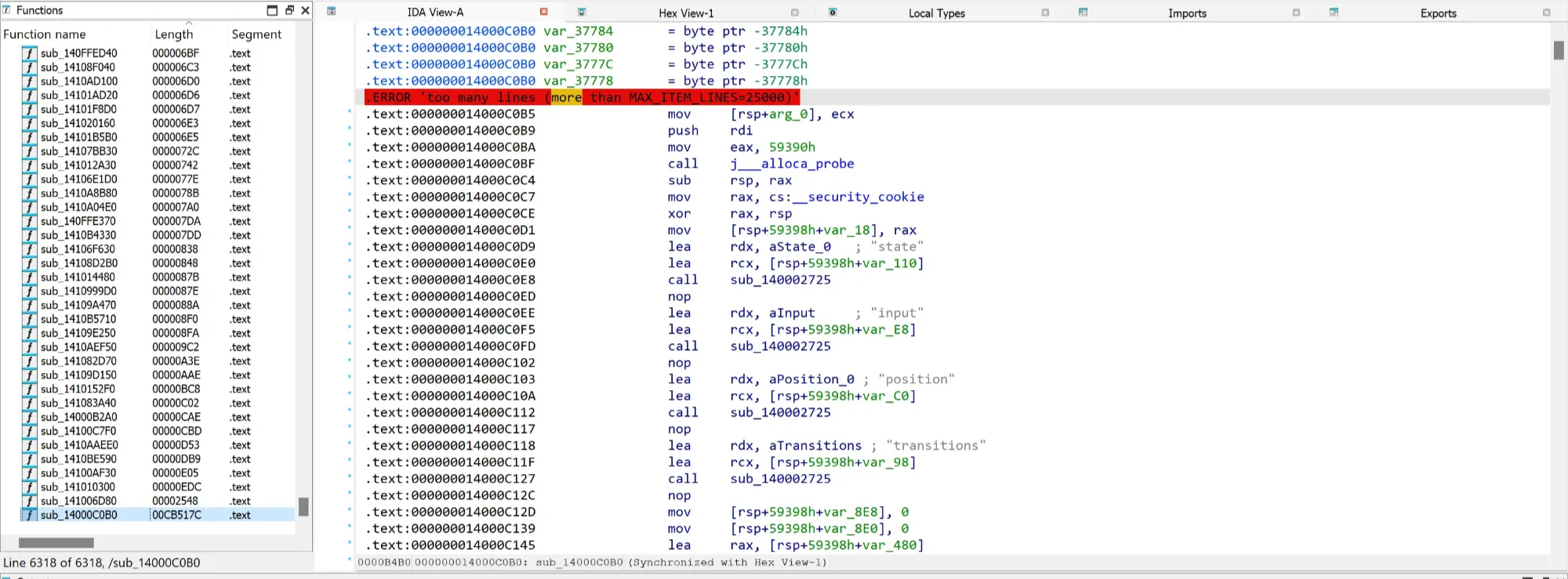
Opening the executable file in IDA is painfully slow. Sorting the functions by length reveals sub_14000C0B0 of approximately 833 KB in size, which is unusually large for a function. This function appears to be implementing a finite state machine (that’s probably what fsm in ntfsm stands for) for validating an input password.
At the time of writing this I don’t remember how I figured this out as a finite state machine (FSM) though. Maybe I was using Claude to help me with understanding some disassembly earlier and it took me to start searching for FSM after that LOL.
I just came across some code and ended up at 0x140C687B8 where I found a massive jump table jpt_14000CA5A. IDA told me that this jumptable has like 65k+ cases!
I wasn’t able to decompile this function even though I tried to increase the function size limits. I guess it’s probably because of all these jump table stuff cramming inside this function.
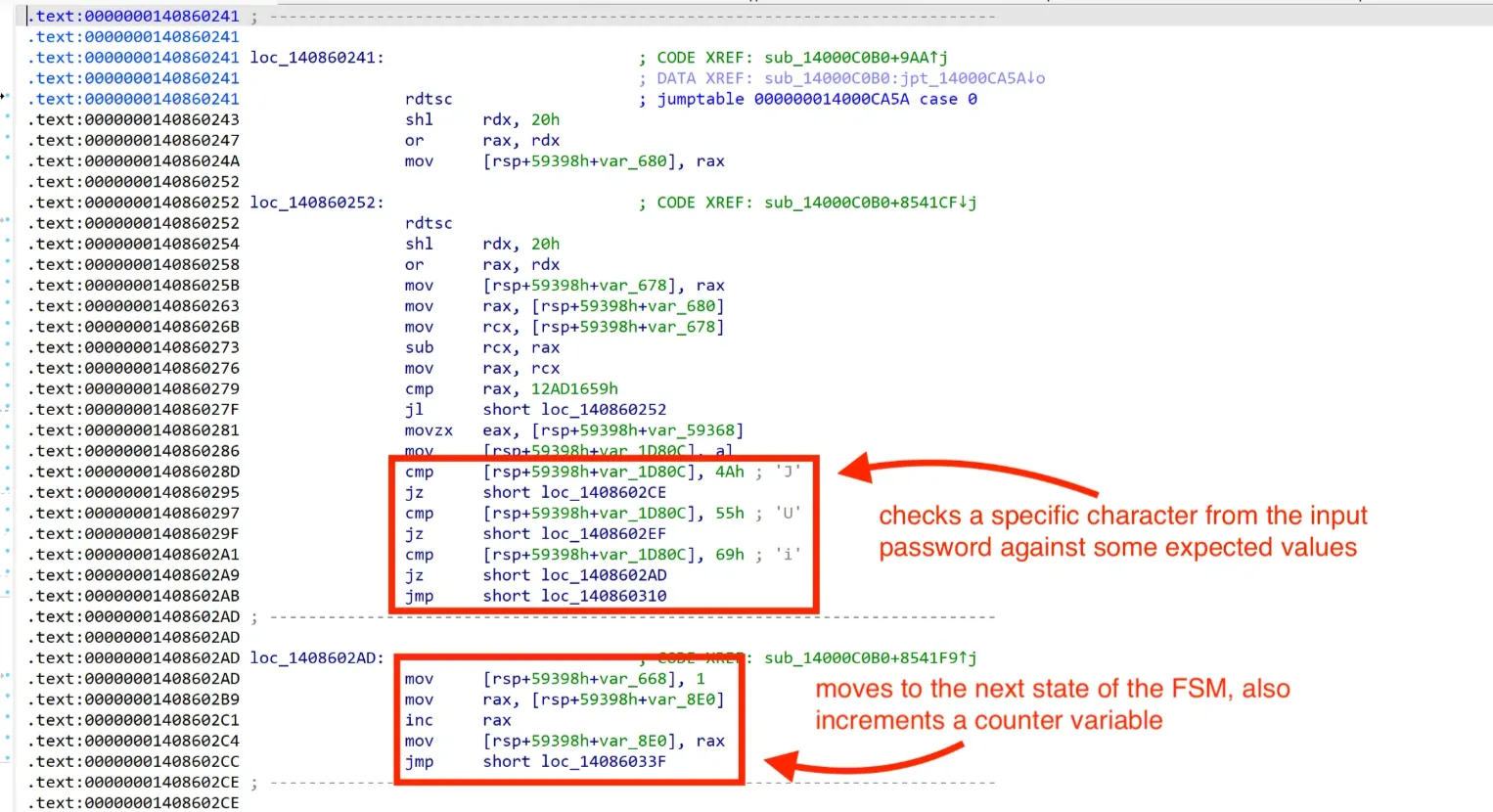
Let’s poke around some cases of the jump table! Looking at case 0 at loc_140860241, each case must be a state of the FSM, which checks a specific character from the input password against some expected values, and finally moves to the next states of the FSM accordingly. So the FSM is stored as a giant switch statement with one case per state.
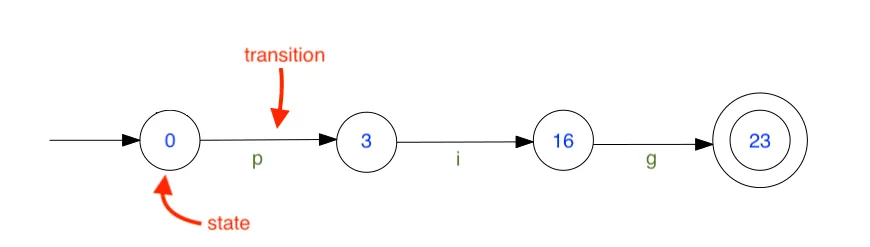
A finite state machine?
I’m going to simplify this term a little bit. This is probably the simplest illustration of a FSM that I have. With an FSM we’ll start at a state (numbered as 0, 1, 2, etc), transition (marked as an arbitrary character) to the next state, and stop at the deepest state.
In this write-up, the FSM is exactly like that. A state is a case in the switch statement (e.g., case 0, case 1), while a transition is moving from one state to another based on an input character (e.g., if we're in state 0 and the input is 'i', we transition to state 1). The password is the sequence of characters that creates 16 valid transitions.
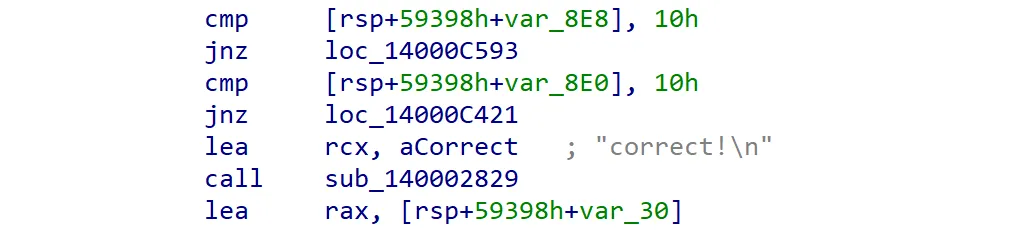
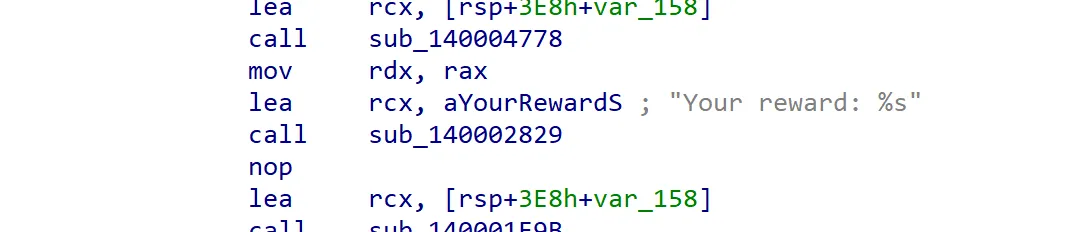
I went back to the beginning of sub_14000C0B0, and found these checks prior to the correct!\n string. These seems to be the conditions needed for the password to be valid.
There’s var_8E8, seems like it’s just storing the number of characters of the input password; so the code here validates if the password is exactly 16 (0x10) characters. Also var_8E0 is the counter variable that gets incremented at every state; the program was using it for checking if there are also exactly 16 transitions occurred; if this is true, the program might reveal the flag.
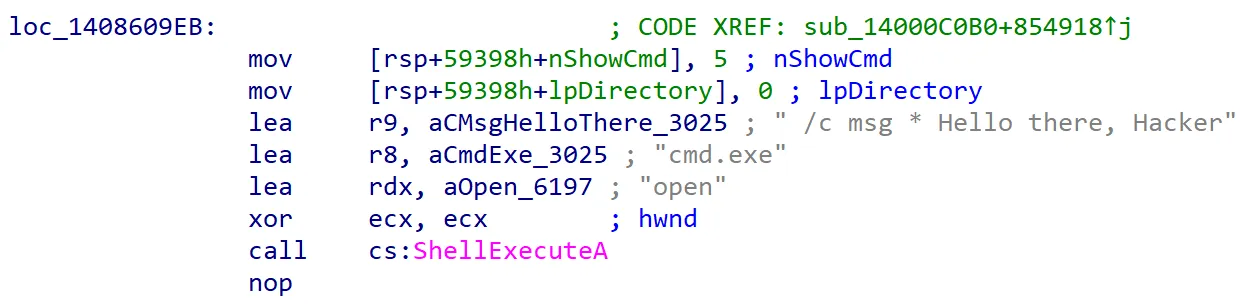
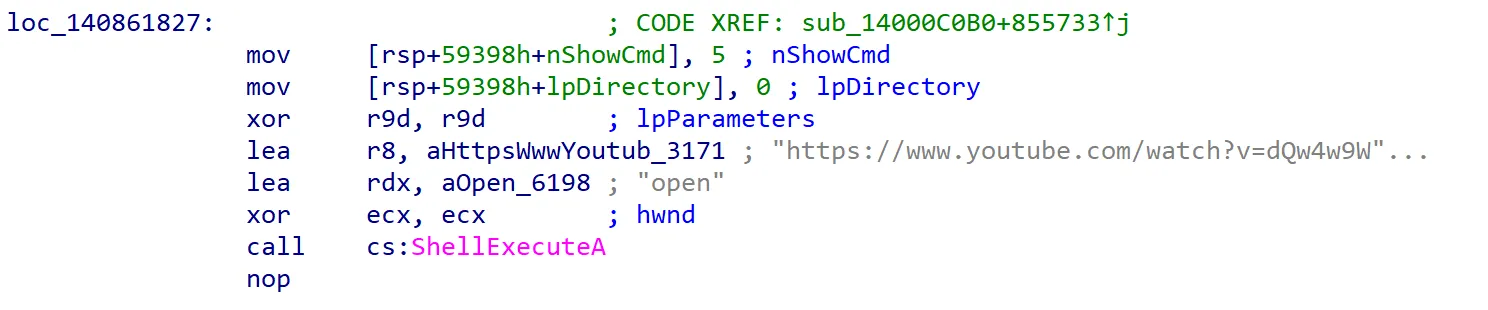
I remembered getting some weird message boxes and random logouts after inputting some random passwords, so I get to some cases to check. These are “dead-end” states where they have no transitions at all. Each “dead-end” state never moves to the next state and just outrageously becomes annoying:
Then I got to some part where the flag is being constructed I guess…
At the end of sub_14000C0B0, seems like the correct password is used to create a SHA-256 hash. This hash is then used as the key to AES-decrypt some blob. The decrypted text is likely to be our flag, which gets printed out as Your reward: %s.
At this point I guess we’ll need to map the FSM into a complete graph structure to find the password. So that’s enough of poking around, let’s do the work.
Mapping The FSM
With over 65k states and multiple branches at each state, manually tracing through the code is impossible. The annoyances added to the program also make it difficult to do brute-forcing as well. So I’ll be approaching the mapping work algorithmically, from building the searchable graph to finding a valid path to the 17th state. At that point, I think we can construct the password by joining the 16 transitions together!
There’s A Pattern?
I started examining several case blocks and identified a consistent pattern. Each state of the FSM follows this structure:
; Load input character
movzx eax, [rsp+59398h+var_59368]
mov [rsp+59398h+var_XXXXX], al ; Store to unique temp variable
; Character comparison 1
cmp [rsp+59398h+var_XXXXX], 'J'
jz loc_YYYY ; Jump if matches
; Character comparison 2
cmp [rsp+59398h+var_XXXXX], 'U'
jz loc_ZZZZ ; Jump if matches
; ... more comparisons ...
; For each match location:
loc_YYYY:
mov [rsp+59398h+var_668], 1 ; Set next state
mov rax, [rsp+59398h+var_8E0]
inc rax ; Increment counter
mov [rsp+59398h+var_8E0], rax
jmp exit_locationI think I know how to extract the transitions!
- First scan for
movzx/movsx eax, [rsp+59398h+var_59368], followed bymov [rsp+59398h+var_XXXXX], alto identify which temporary variables hold the input character. - Then, look for
cmp [rsp+59398h+var_XXXXX], <value>instructions. - After each
cmp, the next instruction should bejzor similar. We need to follow that jump target. At the jump target, scan formov [rsp+59398h+var_668], <next_state>to find where that character leads. Eachcmp/jzpair must be followed individually to correctly map which character leads to which next state.
Doing all of that can help us map something like this:
stateDiagram-v2
[*] --> current_state
current_state --> next_state_1: character_1
current_state --> next_state_2: character_2
current_state --> next_state_3: character_3We can then get to the next states and repeat the same process. When all states are done, we can have the entire map of the FSM!
I’m going to abuse IDA at this point and make an IDAPython script to do all of this.
The Extraction Function
I’m not going into detail for this one, but here’s the extraction function. It should follow the extraction logic that I’ve explained above! I also added checks for various jump/mov instructions to be sure as well, but these additions might be irrelevant.
The function would return an array of transitions containing the next state and the corresponding character of the transition for a given input state.
def extract_transitions_from_case(case_addr):
"""Extract transitions by following conditional jumps"""
transitions = []
ea = case_addr
max_scan = 400
input_vars = set()
# First pass: find all input variable names
scan_ea = ea
for i in range(max_scan):
if scan_ea == idc.BADADDR:
break
mnem = idc.print_insn_mnem(scan_ea)
# Look for: movzx/movsx eax, [rsp+59398h+var_59368]
if mnem in ["movzx", "movsx"]:
op1 = idc.print_operand(scan_ea, 1)
if "var_59368" in op1:
next_ea = idc.next_head(scan_ea)
# Next should be: mov [rsp+59398h+var_XXXXX], al
if idc.print_insn_mnem(next_ea) == "mov":
dest = idc.print_operand(next_ea, 0)
if "var_" in dest and '[' in dest:
# Extract variable name from operand
bracket_content = dest.split('[')[-1].split(']')[0]
if '+' in bracket_content:
var_name = bracket_content.split('+')[-1]
input_vars.add(var_name)
# Stop at common exit
if mnem == "jmp" and "loc_140C685EE" in idc.print_operand(scan_ea, 0):
break
scan_ea = idc.next_head(scan_ea)
# Second pass: find cmp + conditional jump + next state
scan_ea = ea
for i in range(max_scan):
if scan_ea == idc.BADADDR:
break
mnem = idc.print_insn_mnem(scan_ea)
# Look for: cmp [rsp+59398h+var_XXXXX], <char>
if mnem == "cmp":
op0 = idc.print_operand(scan_ea, 0)
# Check if comparing any input variable
if any(var in op0 for var in input_vars):
char_val = idc.get_operand_value(scan_ea, 1)
# Next instruction should be conditional jump
next_ea = idc.next_head(scan_ea)
next_mnem = idc.print_insn_mnem(next_ea)
if next_mnem in ["jz", "jnz", "je", "jne"]:
# Get where the jump goes
jump_target = idc.get_operand_value(next_ea, 0)
# Scan jump target for next state assignment
target_ea = jump_target
for j in range(20):
if target_ea == idc.BADADDR:
break
# Look for: mov [rsp+59398h+var_668], <next_state>
if idc.print_insn_mnem(target_ea) == "mov":
dest = idc.print_operand(target_ea, 0)
if "var_668" in dest:
next_state = idc.get_operand_value(target_ea, 1)
char_str = chr(char_val) if 32 <= char_val < 127 else f"\\x{char_val:02x}"
transitions.append((char_str, next_state))
break
target_ea = idc.next_head(target_ea)
if mnem == "jmp" and "loc_140C685EE" in idc.print_operand(scan_ea, 0):
break
scan_ea = idc.next_head(scan_ea)
return transitionsBuilding The Full FSM
So I got the extraction function. This is now just a matter of using some basic graph algorithms so I’ll be using Claude to help with building the FSM. Claude suggested using breadth-first search starting from state 0:
def build_fsm():
print("[*] Building FSM...")
fsm = {}
visited = set()
to_visit = [0] # Start from initial state
while to_visit:
state = to_visit.pop(0)
if state in visited or state < 0 or state > 65535:
continue
visited.add(state)
# Get code address for this state from jump table
case_addr = get_case_location_from_state(state)
if case_addr < 0x140000000 or case_addr > 0x150000000:
continue
# Extract all transitions from this state
transitions = extract_transitions_from_case(case_addr)
if transitions:
fsm[state] = transitions
print(f"[+] State {state:5d}: {transitions}")
# Add next states to queue
for char, next_state in transitions:
if next_state not in visited:
to_visit.append(next_state)
return fsmBy the way, for this to work we need to find the exact address for a state from the jump table. The jump table is located at 0x140C687B8, and each 4-byte entry contains an offset from base address 0x140000000 to the code for that state. This function can help:
def get_case_location_from_state(state):
jumptable_start = 0x140C687B8
entry_addr = jumptable_start + (state * 4)
offset_val = idc.get_wide_dword(entry_addr)
base = 0x140000000
target_addr = base + offset_val
return target_addrFinding The Password
Alright now I have the complete FSM, I’ll need to find a path of exactly 16 transitions from state 0. I asked Claude again and it gave me some depth-first search code:
def find_path(fsm):
def dfs(state, path, depth):
# Found a complete path
if depth == 16:
return [path[:]]
# No transitions from this state
if state not in fsm or not fsm[state]:
return []
results = []
# Try each possible transition
for char, next_state in fsm[state]:
path.append((state, char, next_state))
results.extend(dfs(next_state, path, depth + 1))
path.pop() # Backtrack
return results
return dfs(0, [], 0)In simple terms, this algorithm explores all branches and backtracks when it hits “dead-end” states. For each valid path found, we extract the password by concatenating the characters:
for path in paths:
password = ''.join([char for _, char, _ in path])
print(f"Password: {password}")Putting Everything Together
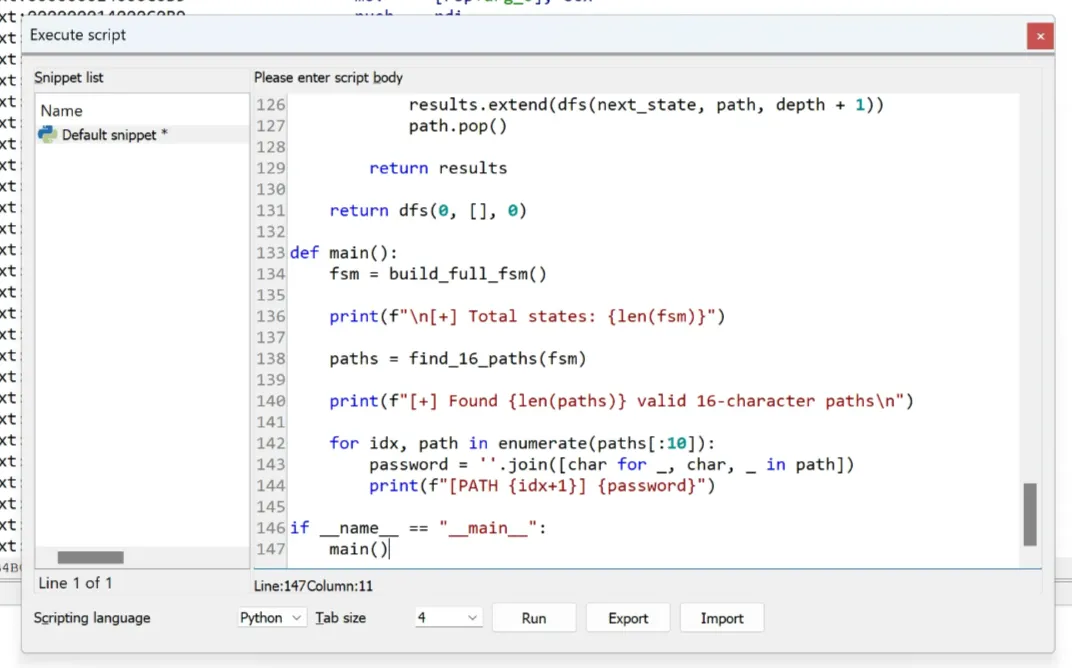
Here’s how the complete IDAPython script should look like. Time to run it!
import idaapi
import idc
import idautils
def get_case_location_from_state(state):
jumptable_start = 0x140C687B8
entry_addr = jumptable_start + (state * 4)
offset_val = idc.get_wide_dword(entry_addr)
base = 0x140000000
target_addr = base + offset_val
return target_addr
def extract_transitions_from_case(case_addr):
transitions = []
ea = case_addr
max_scan = 400
input_vars = set()
scan_ea = ea
for i in range(max_scan):
if scan_ea == idc.BADADDR:
break
mnem = idc.print_insn_mnem(scan_ea)
if mnem in ["movzx", "movsx"]:
op1 = idc.print_operand(scan_ea, 1)
if "var_59368" in op1:
next_ea = idc.next_head(scan_ea)
if idc.print_insn_mnem(next_ea) == "mov":
dest = idc.print_operand(next_ea, 0)
if "var_" in dest and '[' in dest:
bracket_content = dest.split('[')[-1].split(']')[0]
if '+' in bracket_content:
var_name = bracket_content.split('+')[-1]
input_vars.add(var_name)
if mnem == "jmp" and "loc_140C685EE" in idc.print_operand(scan_ea, 0):
break
scan_ea = idc.next_head(scan_ea)
scan_ea = ea
for i in range(max_scan):
if scan_ea == idc.BADADDR:
break
mnem = idc.print_insn_mnem(scan_ea)
if mnem == "cmp":
op0 = idc.print_operand(scan_ea, 0)
if any(var in op0 for var in input_vars):
char_val = idc.get_operand_value(scan_ea, 1)
next_ea = idc.next_head(scan_ea)
next_mnem = idc.print_insn_mnem(next_ea)
if next_mnem in ["jz", "jnz", "je", "jne"]:
jump_target = idc.get_operand_value(next_ea, 0)
target_ea = jump_target
for j in range(20):
if target_ea == idc.BADADDR:
break
if idc.print_insn_mnem(target_ea) == "mov":
dest = idc.print_operand(target_ea, 0)
if "var_668" in dest:
next_state = idc.get_operand_value(target_ea, 1)
char_str = chr(char_val) if 32 <= char_val < 127 else f"\\x{char_val:02x}"
transitions.append((char_str, next_state))
break
target_ea = idc.next_head(target_ea)
if mnem == "jmp" and "loc_140C685EE" in idc.print_operand(scan_ea, 0):
break
scan_ea = idc.next_head(scan_ea)
return transitions
def build_fsm():
print("[*] Building FSM...")
fsm = {}
visited = set()
to_visit = [0]
while to_visit:
state = to_visit.pop(0)
if state in visited or state < 0 or state > 65535:
continue
visited.add(state)
case_addr = get_case_location_from_state(state)
if case_addr < 0x140000000 or case_addr > 0x150000000:
continue
transitions = extract_transitions_from_case(case_addr)
if transitions:
fsm[state] = transitions
print(f"[+] State {state:5d}: {transitions}")
for char, next_state in transitions:
if next_state not in visited:
to_visit.append(next_state)
return fsm
def find_paths(fsm):
print("\n[*] Finding 16-character paths...")
def dfs(state, path, depth):
if depth == 16:
return [path[:]]
if state not in fsm:
return []
results = []
for char, next_state in fsm[state]:
path.append((state, char, next_state))
results.extend(dfs(next_state, path, depth + 1))
path.pop()
return results
return dfs(0, [], 0)
def main():
fsm = build_fsm()
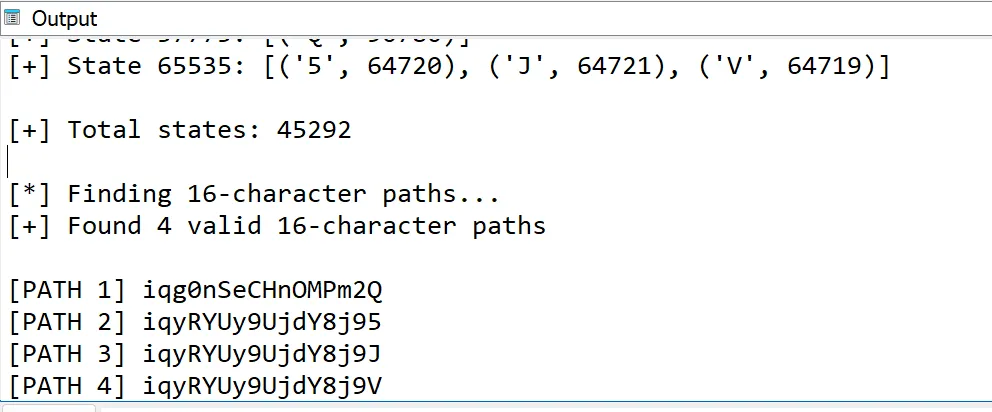
print(f"\n[+] Total states: {len(fsm)}")
paths = find_paths(fsm)
print(f"[+] Found {len(paths)} valid 16-character paths\n")
for idx, path in enumerate(paths[:10]):
password = ''.join([char for _, char, _ in path])
print(f"[PATH {idx+1}] {password}")
if __name__ == "__main__":
main()I’m going to head to IDA and go to File → Script command. Paste the script into the editor, remember to set the Scripting language to Python, and click Run.
After a bit of waiting, I looked at the output console and got 4 different passwords. Wait I thought there is only one correct password but I just got 4 of them!
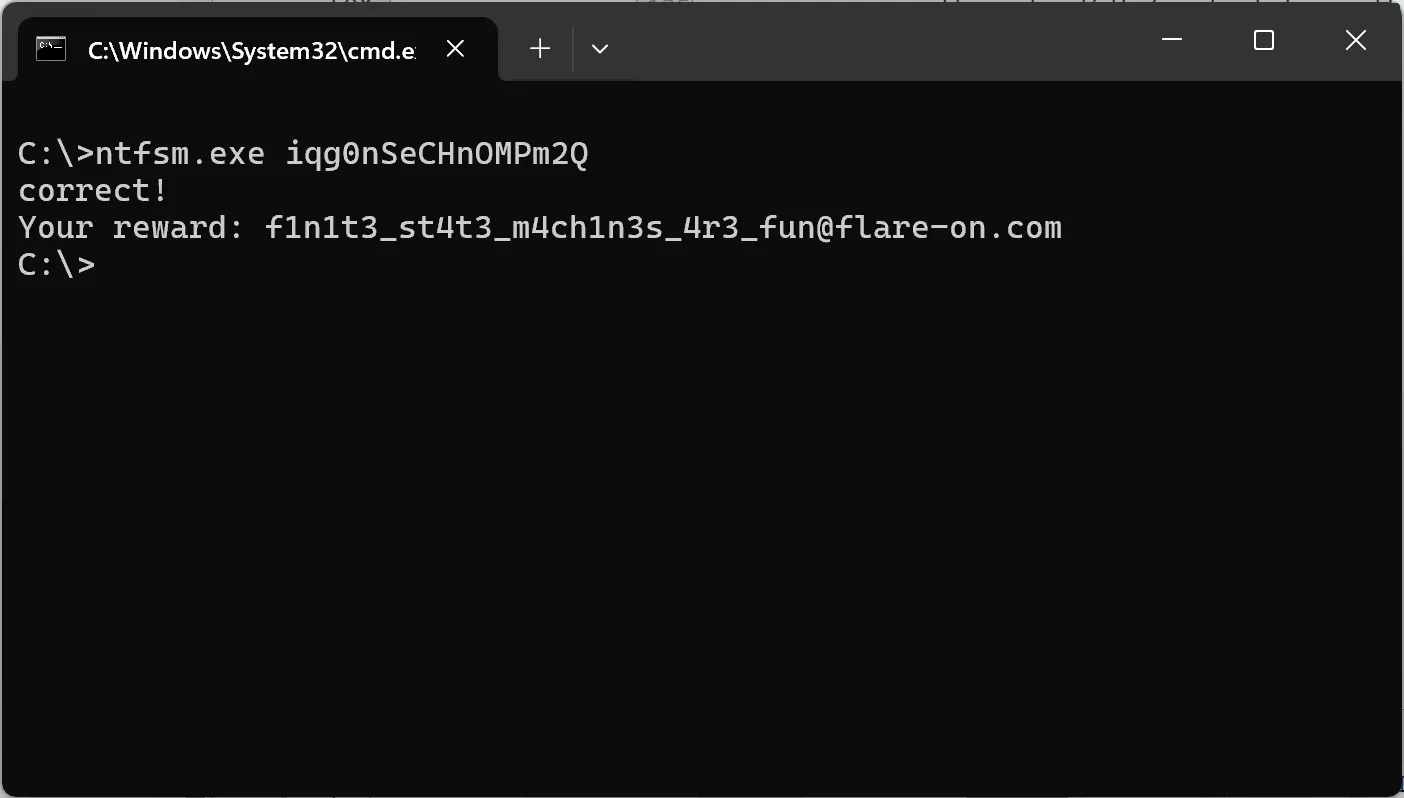
I’ll just go with the first password, iqg0nSeCHnOMPm2Q, and got the flag! Also the other 3 passwords didn’t work, so maybe the my extraction function is just flawed I guess…
f1n1t3_st4t3_m4ch1n3s_4r3_fun@flare-on.com Thoughts
This was my first time playing a reversing CTF. I’ve seen people solving this challenge dynamically, but I just went with static analysis since I didn’t have any prior knowledge of using a debugger at the time of solving this challenge. I got stuck for several days trying to implement solving script since it kept spitting out paths that were either too short or just hit a dead end. After lots of trial and error, I was genuinely surprised to finally get the flag. It was an incredibly satisfying moment!