Challenge Exploration
The challenge gives us an ELF executable called chat_client.
I couldn't run the binary file, so I used the file command to check what I was working with. It turned out to be an x86-64 binary, and since my machine has an ARM processor, I can't execute it directly without using emulation or translation software.
$ file chat_client
chat_client: ELF 64-bit LSB executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, for GNU/Linux 3.2.0, BuildID[sha1]=81544629ae0a32249a48b0bc5134fb7b1455adea, strippedThe only thing I can do now is to solve this problem without knowing what the binary does.
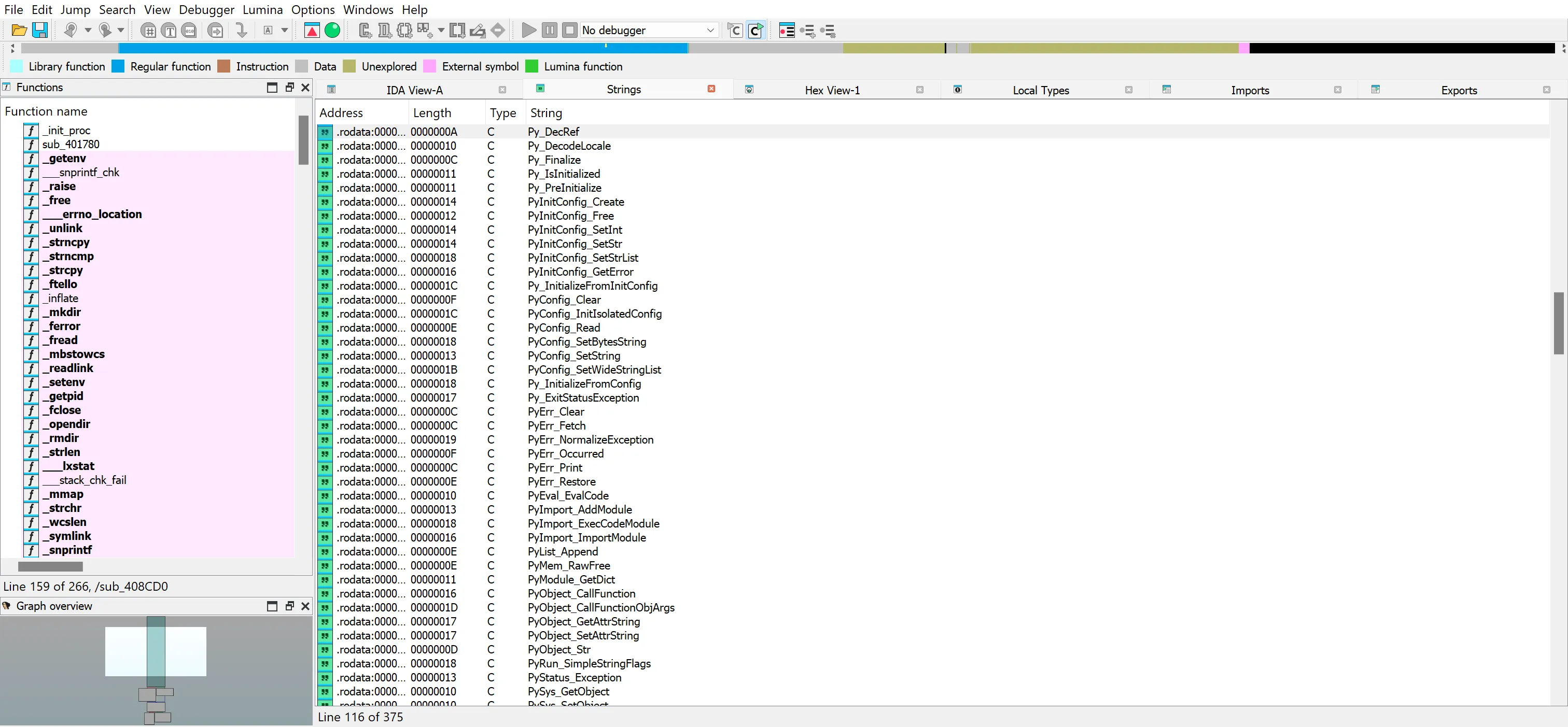
After opening the binary in IDA and digging through a bunch of functions, I was still lost. Then I checked the Strings view and noticed a lot of strings starting with py...
Seems like this could be a Python program packed using PyInstaller! But first, let’s check if this binary has a pydata section using the readelf command:
$ readelf -S chat_client
There are 29 section headers, starting at offset 0x1e86c80:
Section Headers:
[Nr] Name Type Address Offset
Size EntSize Flags Link Info Align
[ 0] NULL 0000000000000000 00000000
0000000000000000 0000000000000000 0 0 0
[ 1] .interp PROGBITS 0000000000400238 00000238
000000000000001c 0000000000000000 A 0 0 1
[ 2] .note.ABI-tag NOTE 0000000000400254 00000254
0000000000000020 0000000000000000 A 0 0 4
[ 3] .note.gnu.bu[...] NOTE 0000000000400274 00000274
0000000000000024 0000000000000000 A 0 0 4
[ 4] .gnu.hash GNU_HASH 0000000000400298 00000298
0000000000000028 0000000000000000 A 5 0 8
[ 5] .dynsym DYNSYM 00000000004002c0 000002c0
0000000000000810 0000000000000018 A 6 1 8
[ 6] .dynstr STRTAB 0000000000400ad0 00000ad0
0000000000000335 0000000000000000 A 0 0 1
[ 7] .gnu.version VERSYM 0000000000400e06 00000e06
00000000000000ac 0000000000000002 A 5 0 2
[ 8] .gnu.version_r VERNEED 0000000000400eb8 00000eb8
00000000000000b0 0000000000000000 A 6 3 8
[ 9] .rela.dyn RELA 0000000000400f68 00000f68
0000000000000060 0000000000000018 A 5 0 8
[10] .rela.plt RELA 0000000000400fc8 00000fc8
0000000000000798 0000000000000018 AI 5 23 8
[11] .init PROGBITS 0000000000401760 00001760
0000000000000017 0000000000000000 AX 0 0 4
[12] .plt PROGBITS 0000000000401780 00001780
0000000000000520 0000000000000010 AX 0 0 16
[13] .text PROGBITS 0000000000401ca0 00001ca0
00000000000083d2 0000000000000000 AX 0 0 16
[14] .fini PROGBITS 000000000040a074 0000a074
0000000000000009 0000000000000000 AX 0 0 4
[15] .rodata PROGBITS 000000000040a080 0000a080
00000000000024f9 0000000000000000 A 0 0 8
[16] .eh_frame_hdr PROGBITS 000000000040c57c 0000c57c
000000000000030c 0000000000000000 A 0 0 4
[17] .eh_frame PROGBITS 000000000040c888 0000c888
0000000000001558 0000000000000000 A 0 0 8
[18] .init_array INIT_ARRAY 000000000060ed90 0000ed90
0000000000000008 0000000000000008 WA 0 0 8
[19] .fini_array FINI_ARRAY 000000000060ed98 0000ed98
0000000000000008 0000000000000008 WA 0 0 8
[20] .data.rel.ro PROGBITS 000000000060eda0 0000eda0
0000000000000048 0000000000000000 WA 0 0 16
[21] .dynamic DYNAMIC 000000000060ede8 0000ede8
0000000000000200 0000000000000010 WA 6 0 8
[22] .got PROGBITS 000000000060efe8 0000efe8
0000000000000010 0000000000000008 WA 0 0 8
[23] .got.plt PROGBITS 000000000060f000 0000f000
00000000000002a0 0000000000000008 WA 0 0 8
[24] .data PROGBITS 000000000060f2a0 0000f2a0
0000000000000010 0000000000000000 WA 0 0 8
[25] .bss NOBITS 000000000060f2c0 0000f2b0
00000000000040b0 0000000000000000 WA 0 0 32
[26] .comment PROGBITS 0000000000000000 0000f2b0
0000000000000029 0000000000000001 MS 0 0 1
[27] pydata PROGBITS 0000000000000000 0000f2d9
0000000001e7789e 0000000000000000 0 0 1
[28] .shstrtab STRTAB 0000000000000000 01e86b77
0000000000000107 0000000000000000 0 0 1
Key to Flags:
W (write), A (alloc), X (execute), M (merge), S (strings), I (info),
L (link order), O (extra OS processing required), G (group), T (TLS),
C (compressed), x (unknown), o (OS specific), E (exclude),
D (mbind), l (large), p (processor specific)Seeing the pydata section, this binary is definitely PyInstaller-generated. Let’s try to revert this back to the original Python source code!
Unpacking The Executable
For this, I’m going to use the pyinstxtractor-ng tool found here:
With some simple commands, we can easily unpack the executable:
$ git clone https://github.com/pyinstxtractor/pyinstxtractor-ng.git
$ cd pyinstxtractor-ng
$ pip install -r requirements.txt
$ python pyinstxtractor_ng.py chat_clientAfter extraction, a folder named chat_client_extracted should appear beside chat_client. Opening it reveals two suspicious files: challenge_to_compile.pyc and chat_log.json.
Upon inspecting the JSON file, we can know that this is some kind of chatting app with some cryptography algorithms.
[
{
"conversation_time": 0,
"mode": "LCG-XOR",
"plaintext": "Hello",
"ciphertext": "e934b27119f12318fe16e8cd1c1678fd3b0a752eca163a7261a7e2510184bbe9"
},
{
"conversation_time": 4,
"mode": "LCG-XOR",
"plaintext": "How are you?",
"ciphertext": "25bf2fd1198392f4935dcace7d747c1e0715865b21358418e67f94163513eae4"
},
{
"conversation_time": 11,
"mode": "LCG-XOR",
"plaintext": "Terrible...",
"ciphertext": "c9f20e5561acf172305cf8f04c13e643c988aa5ab29b5499c93df112687c8c7c"
},
{
"conversation_time": 13,
"mode": "LCG-XOR",
"plaintext": "Is this a secure channel?",
"ciphertext": "3ab9c9f38e4f767a13b12569cdbf13db6bbb939e4c8a57287fb0c9def0288e46"
},
{
"conversation_time": 16,
"mode": "LCG-XOR",
"plaintext": "Yes, it's on the blockchain.",
"ciphertext": "3f6de0c2063d3e8e875737046fef079d73cc9b1b7a4b7b94da2d2867493f6fc5"
},
{
"conversation_time": 24,
"mode": "LCG-XOR",
"plaintext": "Erm enable super safe mode",
"ciphertext": "787cf6c0be39caa21b7908fcd1beca68031b7d11130005ba361c5d361b106b6d"
},
{
"conversation_time": 30,
"mode": "LCG-XOR",
"plaintext": "Ok, activating now",
"ciphertext": "632ab61849140655e0ee6f90ab00b879a3a3da241d4b50bab99f74f169d456db"
},
{
"conversation_time": 242,
"mode": "RSA",
"plaintext": "[ENCRYPTED]",
"ciphertext": "680a65364a498aa87cf17c934ab308b2aee0014aee5b0b7d289b5108677c7ad1eb3bcfbcad7582f87cb3f242391bea7e70e8c01f3ad53ac69488713daea76bb3a524bd2a4bbbc2cfb487477e9d91783f103bd6729b15a4ae99cb93f0db22a467ce12f8d56acaef5d1652c54f495db7bc88aa423bc1c2b60a6ecaede2f4273f6dce265f6c664ec583d7bd75d2fb849d77fa11d05de891b5a706eb103b7dbdb4e5a4a2e72445b61b83fd931cae34e5eaab931037db72ba14e41a70de94472e949ca3cf2135c2ccef0e9b6fa7dd3aaf29a946d165f6ca452466168c32c43c91f159928efb3624e56430b14a0728c52f2668ab26f837120d7af36baf48192ceb3002"
},
{
"conversation_time": 249,
"mode": "RSA",
"plaintext": "[ENCRYPTED]",
"ciphertext": "6f70034472ce115fc82a08560bd22f0e7f373e6ef27bca6e4c8f67fedf4031be23bf50311b4720fe74836b352b34c42db46341cac60298f2fa768f775a9c3da0c6705e0ce11d19b3cbdcf51309c22744e96a19576a8de0e1195f2dab21a3f1b0ef5086afcffa2e086e7738e5032cb5503df39e4bf4bdf620af7aa0f752dac942be50e7fec9a82b63f5c8faf07306e2a2e605bb93df09951c8ad46e5a2572e333484cae16be41929523c83c0d4ca317ef72ea9cde1d5630ebf6c244803d2dc1da0a1eefaafa82339bf0e6cf4bf41b1a2a90f7b2e25313a021eafa6234643acb9d5c9c22674d7bc793f1822743b48227a814a7a6604694296f33c2c59e743f4106"
}
]It’s obvious that we’ll be dealing with a cryptography challenge. But first, we need to disassemble the .pyc file into bytecode, and maybe decompile it into human-readable code.
Decompiling The Bytecode
While common tools like uncompyle6 can perform this task, they no longer support Python 3.9 or newer. After some research, I found Decompyle++, which is actively maintained and likely capable of handling this.
Uhh the build guide isn’t very clear I guess… but let’s try to figure it out by intuition:
$ git clone https://github.com/zrax/pycdc
$ cd pycdc
$ mkdir build
$ cd build
$ cmake ..
$ makeAlright, the project’s built! Now run one last command — sudo make install — so we can call pycdc from anywhere. Since pycdc is the decompiler for these Python bytecode, we can use it to recover the source code of challenge_to_compile.pyc:
$ pycdc challenge_to_compile.pyc > challenge.py
Unsupported opcode: PUSH_EXC_INFO (105)
Unsupported opcode: PUSH_EXC_INFO (105)
Unsupported opcode: BEFORE_WITH (108)
Unsupported opcode: BEFORE_WITH (108)
Unsupported opcode: MAKE_CELL (225)You might see some Unsupported opcode errors during decompilation. That’s normal and usually happens because of differences in bytecode between Python versions. I knew that this can be resolved easily, but it’s not worth doing since we can always look at the original bytecode for parts where decompilation fails later!
In the generated source code, some parts are only partially recovered, but they seem unrelated to the cryptography part we need to focus on, which is great I guess…
# Source Generated with Decompyle++
# File: challenge_to_compile.pyc (Python 3.12)
import tkinter as tk
from tkinter import scrolledtext, messagebox, simpledialog, Checkbutton, BooleanVar, Toplevel
import platform
import hashlib
import time
import json
from threading import Thread
import math
import random
from Crypto.PublicKey import RSA
from Crypto.Util.number import bytes_to_long, long_to_bytes, isPrime
import os
import sys
from web3 import Web3
from eth_account import Account
from eth_account.signers.local import LocalAccount
def resource_path(relative_path):
'''
Get the absolute path to a resource, which works for both development
and for a PyInstaller-bundled executable.
'''
base_path = sys._MEIPASS
return os.path.join(base_path, relative_path)
# WARNING: Decompyle incomplete
class SmartContracts:
rpc_url = ''
private_key = ''
def deploy_contract(contract_bytes, contract_abi):
w3 = Web3(Web3.HTTPProvider(SmartContracts.rpc_url))
if not w3.is_connected():
raise ConnectionError(f'''[!] Failed to connect to Ethereum network at {SmartContracts.rpc_url}''')
print(f'''[+] Connected to Sepolia network at {SmartContracts.rpc_url}''')
print(f'''[+] Current block number: {w3.eth.block_number}''')
if not SmartContracts.private_key:
raise ValueError('Please add your private key.')
account = Account.from_key(SmartContracts.private_key)
w3.eth.default_account = account.address
print(f'''[+] Using account: {account.address}''')
balance_wei = w3.eth.get_balance(account.address)
print(f'''[+] Account balance: {w3.from_wei(balance_wei, 'ether')} ETH''')
if balance_wei == 0:
print('[!] Warning: Account has 0 ETH. Deployment will likely fail. Get some testnet ETH from a faucet (e.g., sepoliafaucet.com)!')
Contract = w3.eth.contract(abi = contract_abi, bytecode = contract_bytes)
gas_estimate = Contract.constructor().estimate_gas()
print(f'''[+] Estimated gas for deployment: {gas_estimate}''')
gas_price = w3.eth.gas_price
print(f'''[+] Current gas price: {w3.from_wei(gas_price, 'gwei')} Gwei''')
transaction = Contract.constructor().build_transaction({
'from': account.address,
'nonce': w3.eth.get_transaction_count(account.address),
'gas': gas_estimate + 200000,
'gasPrice': gas_price })
signed_txn = w3.eth.account.sign_transaction(transaction, private_key = SmartContracts.private_key)
print('[+] Deploying contract...')
tx_hash = w3.eth.send_raw_transaction(signed_txn.raw_transaction)
print(f'''[+] Deployment transaction sent. Hash: {tx_hash.hex()}''')
print('[+] Waiting for transaction to be mined...')
tx_receipt = w3.eth.wait_for_transaction_receipt(tx_hash, timeout = 300)
print(f'''[+] Transaction receipt: {tx_receipt}''')
if tx_receipt.status == 0:
print('[!] Transaction failed (status 0). It was reverted.')
return None
contract_address = tx_receipt.contractAddress
print(f'''[+] Contract deployed at address: {contract_address}''')
deployed_contract = w3.eth.contract(address = contract_address, abi = contract_abi)
return deployed_contract
# WARNING: Decompyle incomplete
class LCGOracle:
def __init__(self, multiplier, increment, modulus, initial_seed):
self.multiplier = multiplier
self.increment = increment
self.modulus = modulus
self.state = initial_seed
self.contract_bytes = '6080604052348015600e575f5ffd5b506102e28061001c5f395ff3fe608060405234801561000f575f5ffd5b5060043610610029575f3560e01c8063115218341461002d575b5f5ffd5b6100476004803603810190610042919061010c565b61005d565b6040516100549190610192565b60405180910390f35b5f5f848061006e5761006d6101ab565b5b86868061007e5761007d6101ab565b5b8987090890505f5f8411610092575f610095565b60015b60ff16905081816100a69190610205565b858260016100b49190610246565b6100be9190610205565b6100c89190610279565b9250505095945050505050565b5f5ffd5b5f819050919050565b6100eb816100d9565b81146100f5575f5ffd5b50565b5f81359050610106816100e2565b92915050565b5f5f5f5f5f60a08688031215610125576101246100d5565b5b5f610132888289016100f8565b9550506020610143888289016100f8565b9450506040610154888289016100f8565b9350506060610165888289016100f8565b9250506080610176888289016100f8565b9150509295509295909350565b61018c816100d9565b82525050565b5f6020820190506101a55f830184610183565b92915050565b7f4e487b71000000000000000000000000000000000000000000000000000000005f52601260045260245ffd5b7f4e487b71000000000000000000000000000000000000000000000000000000005f52601160045260245ffd5b5f61020f826100d9565b915061021a836100d9565b9250828202610228816100d9565b9150828204841483151761023f5761023e6101d8565b5b5092915050565b5f610250826100d9565b915061025b836100d9565b9250828203905081811115610273576102726101d8565b5b92915050565b5f610283826100d9565b915061028e836100d9565b92508282019050808211156102a6576102a56101d8565b5b9291505056fea2646970667358221220c7e885c1633ad951a2d8168f80d36858af279d8b5fe2e19cf79eac15ecb9fdd364736f6c634300081e0033'
self.contract_abi = [
{
'inputs': [
{
'internalType': 'uint256',
'name': 'LCG_MULTIPLIER',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': 'LCG_INCREMENT',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': 'LCG_MODULUS',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': '_currentState',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': '_counter',
'type': 'uint256' }],
'name': 'nextVal',
'outputs': [
{
'internalType': 'uint256',
'name': '',
'type': 'uint256' }],
'stateMutability': 'pure',
'type': 'function' }]
self.deployed_contract = None
def deploy_lcg_contract(self):
self.deployed_contract = SmartContracts.deploy_contract(self.contract_bytes, self.contract_abi)
def get_next(self, counter):
print(f'''\n[+] Calling nextVal() with _currentState={self.state}''')
self.state = self.deployed_contract.functions.nextVal(self.multiplier, self.increment, self.modulus, self.state, counter).call()
print(f''' _counter = {counter}: Result = {self.state}''')
return self.state
class TripleXOROracle:
def __init__(self):
self.contract_bytes = '61030f61004d600b8282823980515f1a6073146041577f4e487b71000000000000000000000000000000000000000000000000000000005f525f60045260245ffd5b305f52607381538281f3fe7300000000000000000000000000000000000000003014608060405260043610610034575f3560e01c80636230075614610038575b5f5ffd5b610052600480360381019061004d919061023c565b610068565b60405161005f91906102c0565b60405180910390f35b5f5f845f1b90505f845f1b90505f61007f85610092565b9050818382181893505050509392505050565b5f5f8290506020815111156100ae5780515f525f5191506100b6565b602081015191505b50919050565b5f604051905090565b5f5ffd5b5f5ffd5b5f819050919050565b6100df816100cd565b81146100e9575f5ffd5b50565b5f813590506100fa816100d6565b92915050565b5f5ffd5b5f5ffd5b5f601f19601f8301169050919050565b7f4e487b71000000000000000000000000000000000000000000000000000000005f52604160045260245ffd5b61014e82610108565b810181811067ffffffffffffffff8211171561016d5761016c610118565b5b80604052505050565b5f61017f6100bc565b905061018b8282610145565b919050565b5f67ffffffffffffffff8211156101aa576101a9610118565b5b6101b382610108565b9050602081019050919050565b828183375f83830152505050565b5f6101e06101db84610190565b610176565b9050828152602081018484840111156101fc576101fb610104565b5b6102078482856101c0565b509392505050565b5f82601f83011261022357610222610100565b5b81356102338482602086016101ce565b91505092915050565b5f5f5f60608486031215610253576102526100c5565b5b5f610260868287016100ec565b9350506020610271868287016100ec565b925050604084013567ffffffffffffffff811115610292576102916100c9565b5b61029e8682870161020f565b9150509250925092565b5f819050919050565b6102ba816102a8565b82525050565b5f6020820190506102d35f8301846102b1565b9291505056fea26469706673582212203fc7e6cc4bf6a86689f458c2d70c565e7c776de95b401008e58ca499ace9ecb864736f6c634300081e0033'
self.contract_abi = [
{
'inputs': [
{
'internalType': 'uint256',
'name': '_primeFromLcg',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': '_conversationTime',
'type': 'uint256' },
{
'internalType': 'string',
'name': '_plaintext',
'type': 'string' }],
'name': 'encrypt',
'outputs': [
{
'internalType': 'bytes32',
'name': '',
'type': 'bytes32' }],
'stateMutability': 'pure',
'type': 'function' }]
self.deployed_contract = None
def deploy_triple_xor_contract(self):
self.deployed_contract = SmartContracts.deploy_contract(self.contract_bytes, self.contract_abi)
def encrypt(self, prime_from_lcg, conversation_time, plaintext_bytes):
print(f'''\n[+] Calling encrypt() with prime_from_lcg={prime_from_lcg}, time={conversation_time}, plaintext={plaintext_bytes}''')
ciphertext = self.deployed_contract.functions.encrypt(prime_from_lcg, conversation_time, plaintext_bytes).call()
print(f''' _ciphertext = {ciphertext.hex()}''')
return ciphertext
class ChatLogic:
def __init__(self):
self.lcg_oracle = None
self.xor_oracle = None
self.rsa_key = None
self.seed_hash = None
self.super_safe_mode = False
self.message_count = 0
self.conversation_start_time = 0
self.chat_history = []
self._initialize_crypto_backend()
def _get_system_artifact_hash(self):
artifact = platform.node().encode('utf-8')
hash_val = hashlib.sha256(artifact).digest()
seed_hash = int.from_bytes(hash_val, 'little')
print(f'''[SETUP] - Generated Seed {seed_hash}...''')
return seed_hash
def _generate_primes_from_hash(self, seed_hash):
primes = []
current_hash_byte_length = (seed_hash.bit_length() + 7) // 8
current_hash = seed_hash.to_bytes(current_hash_byte_length, 'little')
print('[SETUP] Generating LCG parameters from system artifact...')
iteration_limit = 10000
iterations = 0
if len(primes) < 3 and iterations < iteration_limit:
current_hash = hashlib.sha256(current_hash).digest()
candidate = int.from_bytes(current_hash, 'little')
iterations += 1
if candidate.bit_length() == 256 and isPrime(candidate):
primes.append(candidate)
print(f'''[SETUP] - Found parameter {len(primes)}: {str(candidate)[:20]}...''')
if len(primes) < 3 and iterations < iteration_limit:
continue
if len(primes) < 3:
error_msg = '[!] Error: Could not find 3 primes within iteration limit.'
print('Current Primes: ', primes)
print(error_msg)
exit()
return (primes[0], primes[1], primes[2])
def _initialize_crypto_backend(self):
self.seed_hash = self._get_system_artifact_hash()
(m, c, n) = self._generate_primes_from_hash(self.seed_hash)
self.lcg_oracle = LCGOracle(m, c, n, self.seed_hash)
self.lcg_oracle.deploy_lcg_contract()
print('[SETUP] LCG Oracle is on-chain...')
self.xor_oracle = TripleXOROracle()
self.xor_oracle.deploy_triple_xor_contract()
print('[SETUP] Triple XOR Oracle is on-chain...')
print('[SETUP] Crypto backend initialized...')
def generate_rsa_key_from_lcg(self):
print('[RSA] Generating RSA key from on-chain LCG primes...')
lcg_for_rsa = LCGOracle(self.lcg_oracle.multiplier, self.lcg_oracle.increment, self.lcg_oracle.modulus, self.seed_hash)
lcg_for_rsa.deploy_lcg_contract()
primes_arr = []
rsa_msg_count = 0
iteration_limit = 10000
iterations = 0
if len(primes_arr) < 8 and iterations < iteration_limit:
candidate = lcg_for_rsa.get_next(rsa_msg_count)
rsa_msg_count += 1
iterations += 1
if candidate.bit_length() == 256 and isPrime(candidate):
primes_arr.append(candidate)
print(f'''[RSA] - Found 256-bit prime #{len(primes_arr)}''')
if len(primes_arr) < 8 and iterations < iteration_limit:
continue
print('Primes Array: ', primes_arr)
if len(primes_arr) < 8:
error_msg = '[RSA] Error: Could not find 8 primes within iteration limit.'
print('Current Primes: ', primes_arr)
print(error_msg)
return error_msg
n = None
for p_val in primes_arr:
n *= p_val
phi = 1
for p_val in primes_arr:
phi *= p_val - 1
e = 65537
if math.gcd(e, phi) != 1:
error_msg = '[RSA] Error: Public exponent e is not coprime with phi(n). Cannot generate key.'
print(error_msg)
return error_msg
self.rsa_key = None.construct((n, e))
# WARNING: Decompyle incomplete
def process_message(self, plaintext):
if self.conversation_start_time == 0:
self.conversation_start_time = time.time()
conversation_time = int(time.time() - self.conversation_start_time)
if self.super_safe_mode and self.rsa_key:
plaintext_bytes = plaintext.encode('utf-8')
plaintext_enc = bytes_to_long(plaintext_bytes)
_enc = pow(plaintext_enc, self.rsa_key.e, self.rsa_key.n)
ciphertext = _enc.to_bytes(self.rsa_key.n.bit_length(), 'little').rstrip(b'\x00')
encryption_mode = 'RSA'
plaintext = '[ENCRYPTED]'
else:
prime_from_lcg = self.lcg_oracle.get_next(self.message_count)
ciphertext = self.xor_oracle.encrypt(prime_from_lcg, conversation_time, plaintext)
encryption_mode = 'LCG-XOR'
log_entry = {
'conversation_time': conversation_time,
'mode': encryption_mode,
'plaintext': plaintext,
'ciphertext': ciphertext.hex() }
self.chat_history.append(log_entry)
self.save_chat_log()
return (f'''[{conversation_time}s] {plaintext}''', f'''[{conversation_time}s] {ciphertext.hex()}''')
def save_chat_log(self):
pass
# WARNING: Decompyle incomplete
class ChatApp(tk.Tk):
pass
# WARNING: Decompyle incomplete
if __name__ == '__main__':
app = ChatApp()
app.mainloop()
return NoneBreaking Down The Challenge
Let’s go through the chat log JSON and the main components of the generated Python source code to understand how it works and possibly find a way to solve the challenge.
Chat Log JSON File
Inspecting the chat log JSON file reveals how the chatting system works and suggests where the flag might be hidden.
Initially the system uses LCG-XOR to encrypt messages, but the unencrypted plaintext is still given to us along with the ciphertext. After the seventh message it switches to RSA, at which point the last two messages display plaintext as [ENCRYPTED].
I’m going to make a guess that the flag is hidden in those RSA-encrypted message, so we need to find a way to decrypt these messages.
Chat App Components
SmartContracts
At first glance, I figured this would be tough. I don’t know much about blockchain! However, with the help of Grok, I’m starting to make sense of it.
Well this SmartContracts class simply handles the deployment of smart contracts to Etherium, which is a blockchain. It connects to a testnet (Sepolia), signs transactions with a private key, and deploys contracts.
Once again, I don’t know anything about smart contracts or testnet anyways, so if you don’t understand any of this, it’s fine! After some conversations with Grok, it told me that this is just for offloading computations to the blockchain, so I guess we can safely skip this class.
class SmartContracts:
rpc_url = ''
private_key = ''
def deploy_contract(contract_bytes, contract_abi):
w3 = Web3(Web3.HTTPProvider(SmartContracts.rpc_url))
if not w3.is_connected():
raise ConnectionError(f'''[!] Failed to connect to Ethereum network at {SmartContracts.rpc_url}''')
print(f'''[+] Connected to Sepolia network at {SmartContracts.rpc_url}''')
print(f'''[+] Current block number: {w3.eth.block_number}''')
if not SmartContracts.private_key:
raise ValueError('Please add your private key.')
account = Account.from_key(SmartContracts.private_key)
w3.eth.default_account = account.address
print(f'''[+] Using account: {account.address}''')
balance_wei = w3.eth.get_balance(account.address)
print(f'''[+] Account balance: {w3.from_wei(balance_wei, 'ether')} ETH''')
if balance_wei == 0:
print('[!] Warning: Account has 0 ETH. Deployment will likely fail. Get some testnet ETH from a faucet (e.g., sepoliafaucet.com)!')
Contract = w3.eth.contract(abi = contract_abi, bytecode = contract_bytes)
gas_estimate = Contract.constructor().estimate_gas()
print(f'''[+] Estimated gas for deployment: {gas_estimate}''')
gas_price = w3.eth.gas_price
print(f'''[+] Current gas price: {w3.from_wei(gas_price, 'gwei')} Gwei''')
transaction = Contract.constructor().build_transaction({
'from': account.address,
'nonce': w3.eth.get_transaction_count(account.address),
'gas': gas_estimate + 200000,
'gasPrice': gas_price })
signed_txn = w3.eth.account.sign_transaction(transaction, private_key = SmartContracts.private_key)
print('[+] Deploying contract...')
tx_hash = w3.eth.send_raw_transaction(signed_txn.raw_transaction)
print(f'''[+] Deployment transaction sent. Hash: {tx_hash.hex()}''')
print('[+] Waiting for transaction to be mined...')
tx_receipt = w3.eth.wait_for_transaction_receipt(tx_hash, timeout = 300)
print(f'''[+] Transaction receipt: {tx_receipt}''')
if tx_receipt.status == 0:
print('[!] Transaction failed (status 0). It was reverted.')
return None
contract_address = tx_receipt.contractAddress
print(f'''[+] Contract deployed at address: {contract_address}''')
deployed_contract = w3.eth.contract(address = contract_address, abi = contract_abi)
return deployed_contract
# WARNING: Decompyle incompleteLCGOracle
With this class, we’re given a super long smart contract bytecode in hexadecimal form and an ABI interface. Looking at the ABI and the class name as well, I’m pretty sure that this implements a Linear Congruential Generator (LCG).
class LCGOracle:
def __init__(self, multiplier, increment, modulus, initial_seed):
self.multiplier = multiplier
self.increment = increment
self.modulus = modulus
self.state = initial_seed
self.contract_bytes = '6080604052348015600e575f5ffd5b506102e28061001c5f395ff3fe608060405234801561000f575f5ffd5b5060043610610029575f3560e01c8063115218341461002d575b5f5ffd5b6100476004803603810190610042919061010c565b61005d565b6040516100549190610192565b60405180910390f35b5f5f848061006e5761006d6101ab565b5b86868061007e5761007d6101ab565b5b8987090890505f5f8411610092575f610095565b60015b60ff16905081816100a69190610205565b858260016100b49190610246565b6100be9190610205565b6100c89190610279565b9250505095945050505050565b5f5ffd5b5f819050919050565b6100eb816100d9565b81146100f5575f5ffd5b50565b5f81359050610106816100e2565b92915050565b5f5f5f5f5f60a08688031215610125576101246100d5565b5b5f610132888289016100f8565b9550506020610143888289016100f8565b9450506040610154888289016100f8565b9350506060610165888289016100f8565b9250506080610176888289016100f8565b9150509295509295909350565b61018c816100d9565b82525050565b5f6020820190506101a55f830184610183565b92915050565b7f4e487b71000000000000000000000000000000000000000000000000000000005f52601260045260245ffd5b7f4e487b71000000000000000000000000000000000000000000000000000000005f52601160045260245ffd5b5f61020f826100d9565b915061021a836100d9565b9250828202610228816100d9565b9150828204841483151761023f5761023e6101d8565b5b5092915050565b5f610250826100d9565b915061025b836100d9565b9250828203905081811115610273576102726101d8565b5b92915050565b5f610283826100d9565b915061028e836100d9565b92508282019050808211156102a6576102a56101d8565b5b9291505056fea2646970667358221220c7e885c1633ad951a2d8168f80d36858af279d8b5fe2e19cf79eac15ecb9fdd364736f6c634300081e0033'
self.contract_abi = [
{
'inputs': [
{
'internalType': 'uint256',
'name': 'LCG_MULTIPLIER',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': 'LCG_INCREMENT',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': 'LCG_MODULUS',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': '_currentState',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': '_counter',
'type': 'uint256' }],
'name': 'nextVal',
'outputs': [
{
'internalType': 'uint256',
'name': '',
'type': 'uint256' }],
'stateMutability': 'pure',
'type': 'function' }]
self.deployed_contract = None
def deploy_lcg_contract(self):
self.deployed_contract = SmartContracts.deploy_contract(self.contract_bytes, self.contract_abi)
def get_next(self, counter):
print(f'''\n[+] Calling nextVal() with _currentState={self.state}''')
self.state = self.deployed_contract.functions.nextVal(self.multiplier, self.increment, self.modulus, self.state, counter).call()
print(f''' _counter = {counter}: Result = {self.state}''')
return self.stateI spent a little while searching on Google and discovered that these bytecode strings are Ethereum Virtual Machine (EVM) bytecode and can be decompiled into human-readable Solidity-like code. A great decompiler for this would be the one from Dedaub.
I pasted the entire contract_bytes string into the decompiler and it gave me this:
// Note: The function selector is not present in the original solidity code.
// However, we display it for the sake of completeness.
function __function_selector__() public payable {
MEM[64] = 128;
require(!msg.value);
MEM[0:738] = 0x608060405234801561000f575f5ffd5b5060043610610029575f3560e01c8063115218341461002d575b5f5ffd5b6100476004803603810190610042919061010c565b61005d565b6040516100549190610192565b60405180910390f35b5f5f848061006e5761006d6101ab565b5b86868061007e5761007d6101ab565b5b8987090890505f5f8411610092575f610095565b60015b60ff16905081816100a69190610205565b858260016100b49190610246565b6100be9190610205565b6100c89190610279565b9250505095945050505050565b5f5ffd5b5f819050919050565b6100eb816100d9565b81146100f5575f5ffd5b50565b5f81359050610106816100e2565b92915050565b5f5f5f5f5f60a08688031215610125576101246100d5565b5b5f610132888289016100f8565b9550506020610143888289016100f8565b9450506040610154888289016100f8565b9350506060610165888289016100f8565b9250506080610176888289016100f8565b9150509295509295909350565b61018c816100d9565b82525050565b5f6020820190506101a55f830184610183565b92915050565b7f4e487b71000000000000000000000000000000000000000000000000000000005f52601260045260245ffd5b7f4e487b71000000000000000000000000000000000000000000000000000000005f52601160045260245ffd5b5f61020f826100d9565b915061021a836100d9565b9250828202610228816100d9565b9150828204841483151761023f5761023e6101d8565b5b5092915050565b5f610250826100d9565b915061025b836100d9565b9250828203905081811115610273576102726101d8565b5b92915050565b5f610283826100d9565b915061028e836100d9565b92508282019050808211156102a6576102a56101d8565b5b9291505056fea2646970667358221220c7e885c1633ad951a2d8168f80d36858af279d8b5fe2e19cf79eac15ecb9fdd364736f6c634300081e0033;
return MEM[0:738];
}Weird, am I missing something? It turns out that I have to copy the 0x6080... from this code into the decompiler, and it now produces some useful code now LOL.
function _SafeMul(uint256 varg0, uint256 varg1) private {
require(!varg0 | (varg1 == varg0 * varg1 / varg0), Panic(17)); // arithmetic overflow or underflow
return varg0 * varg1;
}
function _SafeSub(uint256 varg0, uint256 varg1) private {
require(varg0 - varg1 <= varg0, Panic(17)); // arithmetic overflow or underflow
return varg0 - varg1;
}
function _SafeAdd(uint256 varg0, uint256 varg1) private {
require(varg0 <= varg0 + varg1, Panic(17)); // arithmetic overflow or underflow
return varg0 + varg1;
}
function fallback() public payable {
revert();
}
function 0x11521834(uint256 varg0, uint256 varg1, uint256 varg2, uint256 varg3, uint256 varg4) public payable {
require(4 + (msg.data.length - 4) - 4 >= 160);
require(varg2, Panic(18)); // division by zero
require(varg2, Panic(18)); // division by zero
if (varg4 > 0) {
v0 = v1 = 1;
} else {
v0 = v2 = 0;
}
v3 = _SafeMul(uint8(v0), (varg3 * varg0 % varg2 + varg1) % varg2);
v4 = _SafeSub(1, uint8(v0));
v5 = _SafeMul(v4, varg3);
v6 = _SafeAdd(v5, v3);
return v6;
}
// Note: The function selector is not present in the original solidity code.
// However, we display it for the sake of completeness.
function __function_selector__( function_selector) public payable {
MEM[64] = 128;
require(!msg.value);
if (msg.data.length >= 4) {
if (0x11521834 == function_selector >> 224) {
0x11521834();
}
}
fallback();
}Upon reading the code, we’re pretty sure that this is indeed an implementation of the LCG. Basically it’s a formula to generate "random" numbers in a predictable pattern:
Here, represents the new state, the current state, the multiplier, the increment, and the modulus. When mapping these the decompiled function 0x11521834(), the parameters varg0, varg1, varg2, and varg3 correspond to the multiplier, increment, modulus, and current state, respectively. The variable varg4 appears to be some counter, though its exact purpose is not yet clear.
If we look at the ABI interface, this 0x11521834() function is defined as nextVal, and varg4 is identified as a counter variable, though its specific role remains unknown at this stage. There’s also the get_next(counter) function which calls the nextVal function to update the state of the LCG.
TripleXOROracle
With this class, we’re going to use the same procedure above to decompile the smart contract.
class TripleXOROracle:
def __init__(self):
self.contract_bytes = '61030f61004d600b8282823980515f1a6073146041577f4e487b71000000000000000000000000000000000000000000000000000000005f525f60045260245ffd5b305f52607381538281f3fe7300000000000000000000000000000000000000003014608060405260043610610034575f3560e01c80636230075614610038575b5f5ffd5b610052600480360381019061004d919061023c565b610068565b60405161005f91906102c0565b60405180910390f35b5f5f845f1b90505f845f1b90505f61007f85610092565b9050818382181893505050509392505050565b5f5f8290506020815111156100ae5780515f525f5191506100b6565b602081015191505b50919050565b5f604051905090565b5f5ffd5b5f5ffd5b5f819050919050565b6100df816100cd565b81146100e9575f5ffd5b50565b5f813590506100fa816100d6565b92915050565b5f5ffd5b5f5ffd5b5f601f19601f8301169050919050565b7f4e487b71000000000000000000000000000000000000000000000000000000005f52604160045260245ffd5b61014e82610108565b810181811067ffffffffffffffff8211171561016d5761016c610118565b5b80604052505050565b5f61017f6100bc565b905061018b8282610145565b919050565b5f67ffffffffffffffff8211156101aa576101a9610118565b5b6101b382610108565b9050602081019050919050565b828183375f83830152505050565b5f6101e06101db84610190565b610176565b9050828152602081018484840111156101fc576101fb610104565b5b6102078482856101c0565b509392505050565b5f82601f83011261022357610222610100565b5b81356102338482602086016101ce565b91505092915050565b5f5f5f60608486031215610253576102526100c5565b5b5f610260868287016100ec565b9350506020610271868287016100ec565b925050604084013567ffffffffffffffff811115610292576102916100c9565b5b61029e8682870161020f565b9150509250925092565b5f819050919050565b6102ba816102a8565b82525050565b5f6020820190506102d35f8301846102b1565b9291505056fea26469706673582212203fc7e6cc4bf6a86689f458c2d70c565e7c776de95b401008e58ca499ace9ecb864736f6c634300081e0033'
self.contract_abi = [
{
'inputs': [
{
'internalType': 'uint256',
'name': '_primeFromLcg',
'type': 'uint256' },
{
'internalType': 'uint256',
'name': '_conversationTime',
'type': 'uint256' },
{
'internalType': 'string',
'name': '_plaintext',
'type': 'string' }],
'name': 'encrypt',
'outputs': [
{
'internalType': 'bytes32',
'name': '',
'type': 'bytes32' }],
'stateMutability': 'pure',
'type': 'function' }]
self.deployed_contract = None
def deploy_triple_xor_contract(self):
self.deployed_contract = SmartContracts.deploy_contract(self.contract_bytes, self.contract_abi)
def encrypt(self, prime_from_lcg, conversation_time, plaintext_bytes):
print(f'''\n[+] Calling encrypt() with prime_from_lcg={prime_from_lcg}, time={conversation_time}, plaintext={plaintext_bytes}''')
ciphertext = self.deployed_contract.functions.encrypt(prime_from_lcg, conversation_time, plaintext_bytes).call()
print(f''' _ciphertext = {ciphertext.hex()}''')
return ciphertextOnce again, we got some nice decompilations:
function fallback() public payable {
revert();
}
function 0x62300756(uint256 varg0, uint256 varg1, bytes varg2) public payable {
require(4 + (msg.data.length - 4) - 4 >= 96);
require(varg2 <= uint64.max);
require(4 + varg2 + 31 < 4 + (msg.data.length - 4));
require(varg2.length <= uint64.max, Panic(65)); // failed memory allocation (too much memory)
v0 = new bytes[](varg2.length);
require(!((v0 + ((varg2.length + 31 & 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffe0) + 32 + 31 & 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffe0) > uint64.max) | (v0 + ((varg2.length + 31 & 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffe0) + 32 + 31 & 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffe0) < v0)), Panic(65)); // failed memory allocation (too much memory)
require(varg2.data + varg2.length <= 4 + (msg.data.length - 4));
CALLDATACOPY(v0.data, varg2.data, varg2.length);
v0[varg2.length] = 0;
if (v0.length <= 32) {
v1 = v2 = MEM[v0.data];
}
return v1 ^ varg0 ^ varg1;
}
// Note: The function selector is not present in the original solidity code.
// However, we display it for the sake of completeness.
function __function_selector__( function_selector) public payable {
MEM[64] = 128;
if (msg.data.length >= 4) {
if (0x62300756 == function_selector >> 224) {
0x62300756();
}
}
fallback();
}Based on the ABI, we can map the parameters of the 0x62300756() function to prime_from_lcg, conversation_time, and plaintext, respectively. Essentially, this function takes the LCG prime, the conversation timestamp, and a plaintext string, then returns the XOR of the two numbers with the decoded 32-byte value from the string’s byte array. There is some right-zero paddings for strings smaller than 32 bytes as well!
Ooh, this is definitely the LCG-XOR encryption that we’ve seen in the chat log! If you look at the chat log, the first 7 values of the plaintext, timestamp, and ciphertext are exposed to us, we can easily recover the primes (or the LCG outputs for message 0 to 6) by doing prime = ciphertext XOR plaintext XOR conversation_time!
Cryptography Backend
This is probably the most important part of the script. This ChatLogic class is responsible for all of the cryptography logic of the chat app itself.
class ChatLogic:
def __init__(self):
self.lcg_oracle = None
self.xor_oracle = None
self.rsa_key = None
self.seed_hash = None
self.super_safe_mode = False
self.message_count = 0
self.conversation_start_time = 0
self.chat_history = []
self._initialize_crypto_backend()
def _get_system_artifact_hash(self):
artifact = platform.node().encode('utf-8')
hash_val = hashlib.sha256(artifact).digest()
seed_hash = int.from_bytes(hash_val, 'little')
print(f'''[SETUP] - Generated Seed {seed_hash}...''')
return seed_hash
def _generate_primes_from_hash(self, seed_hash):
primes = []
current_hash_byte_length = (seed_hash.bit_length() + 7) // 8
current_hash = seed_hash.to_bytes(current_hash_byte_length, 'little')
print('[SETUP] Generating LCG parameters from system artifact...')
iteration_limit = 10000
iterations = 0
if len(primes) < 3 and iterations < iteration_limit:
current_hash = hashlib.sha256(current_hash).digest()
candidate = int.from_bytes(current_hash, 'little')
iterations += 1
if candidate.bit_length() == 256 and isPrime(candidate):
primes.append(candidate)
print(f'''[SETUP] - Found parameter {len(primes)}: {str(candidate)[:20]}...''')
if len(primes) < 3 and iterations < iteration_limit:
continue
if len(primes) < 3:
error_msg = '[!] Error: Could not find 3 primes within iteration limit.'
print('Current Primes: ', primes)
print(error_msg)
exit()
return (primes[0], primes[1], primes[2])
def _initialize_crypto_backend(self):
self.seed_hash = self._get_system_artifact_hash()
(m, c, n) = self._generate_primes_from_hash(self.seed_hash)
self.lcg_oracle = LCGOracle(m, c, n, self.seed_hash)
self.lcg_oracle.deploy_lcg_contract()
print('[SETUP] LCG Oracle is on-chain...')
self.xor_oracle = TripleXOROracle()
self.xor_oracle.deploy_triple_xor_contract()
print('[SETUP] Triple XOR Oracle is on-chain...')
print('[SETUP] Crypto backend initialized...')
def generate_rsa_key_from_lcg(self):
print('[RSA] Generating RSA key from on-chain LCG primes...')
lcg_for_rsa = LCGOracle(self.lcg_oracle.multiplier, self.lcg_oracle.increment, self.lcg_oracle.modulus, self.seed_hash)
lcg_for_rsa.deploy_lcg_contract()
primes_arr = []
rsa_msg_count = 0
iteration_limit = 10000
iterations = 0
if len(primes_arr) < 8 and iterations < iteration_limit:
candidate = lcg_for_rsa.get_next(rsa_msg_count)
rsa_msg_count += 1
iterations += 1
if candidate.bit_length() == 256 and isPrime(candidate):
primes_arr.append(candidate)
print(f'''[RSA] - Found 256-bit prime #{len(primes_arr)}''')
if len(primes_arr) < 8 and iterations < iteration_limit:
continue
print('Primes Array: ', primes_arr)
if len(primes_arr) < 8:
error_msg = '[RSA] Error: Could not find 8 primes within iteration limit.'
print('Current Primes: ', primes_arr)
print(error_msg)
return error_msg
n = None
for p_val in primes_arr:
n *= p_val
phi = 1
for p_val in primes_arr:
phi *= p_val - 1
e = 65537
if math.gcd(e, phi) != 1:
error_msg = '[RSA] Error: Public exponent e is not coprime with phi(n). Cannot generate key.'
print(error_msg)
return error_msg
self.rsa_key = None.construct((n, e))
# WARNING: Decompyle incomplete
def process_message(self, plaintext):
if self.conversation_start_time == 0:
self.conversation_start_time = time.time()
conversation_time = int(time.time() - self.conversation_start_time)
if self.super_safe_mode and self.rsa_key:
plaintext_bytes = plaintext.encode('utf-8')
plaintext_enc = bytes_to_long(plaintext_bytes)
_enc = pow(plaintext_enc, self.rsa_key.e, self.rsa_key.n)
ciphertext = _enc.to_bytes(self.rsa_key.n.bit_length(), 'little').rstrip(b'\x00')
encryption_mode = 'RSA'
plaintext = '[ENCRYPTED]'
else:
prime_from_lcg = self.lcg_oracle.get_next(self.message_count)
ciphertext = self.xor_oracle.encrypt(prime_from_lcg, conversation_time, plaintext)
encryption_mode = 'LCG-XOR'
log_entry = {
'conversation_time': conversation_time,
'mode': encryption_mode,
'plaintext': plaintext,
'ciphertext': ciphertext.hex() }
self.chat_history.append(log_entry)
self.save_chat_log()
return (f'''[{conversation_time}s] {plaintext}''', f'''[{conversation_time}s] {ciphertext.hex()}''')
def save_chat_log(self):
pass
# WARNING: Decompyle incompleteBackend Initialization
Let’s analyze the first two methods.
def _get_system_artifact_hash(self):
artifact = platform.node().encode('utf-8')
hash_val = hashlib.sha256(artifact).digest()
seed_hash = int.from_bytes(hash_val, 'little')
print(f'''[SETUP] - Generated Seed {seed_hash}...''')
return seed_hash
def _generate_primes_from_hash(self, seed_hash):
primes = []
current_hash_byte_length = (seed_hash.bit_length() + 7) // 8
current_hash = seed_hash.to_bytes(current_hash_byte_length, 'little')
print('[SETUP] Generating LCG parameters from system artifact...')
iteration_limit = 10000
iterations = 0
if len(primes) < 3 and iterations < iteration_limit:
current_hash = hashlib.sha256(current_hash).digest()
candidate = int.from_bytes(current_hash, 'little')
iterations += 1
if candidate.bit_length() == 256 and isPrime(candidate):
primes.append(candidate)
print(f'''[SETUP] - Found parameter {len(primes)}: {str(candidate)[:20]}...''')
if len(primes) < 3 and iterations < iteration_limit:
continue
if len(primes) < 3:
error_msg = '[!] Error: Could not find 3 primes within iteration limit.'
print('Current Primes: ', primes)
print(error_msg)
exit()
return (primes[0], primes[1], primes[2])The cryptographic backend first creates a seed by hashing the nodename (or hostname) of the computer that the script is running on, using SHA-256. As a result, this seed is unique per machine, so we can’t get it. The seed is then used to generate three 256-bit prime numbers, which serve as the multiplier, increment, and modulus for the LCGOracle class.
Apparently the contracts for the LCG and TripleXOR are deployed during the ChatLogic initialization as well.
def _initialize_crypto_backend(self):
self.seed_hash = self._get_system_artifact_hash()
(m, c, n) = self._generate_primes_from_hash(self.seed_hash)
self.lcg_oracle = LCGOracle(m, c, n, self.seed_hash)
self.lcg_oracle.deploy_lcg_contract()
print('[SETUP] LCG Oracle is on-chain...')
self.xor_oracle = TripleXOROracle()
self.xor_oracle.deploy_triple_xor_contract()
print('[SETUP] Triple XOR Oracle is on-chain...')
print('[SETUP] Crypto backend initialized...')You might notice that the seed is also used as the initial state for the LCGOracle class.
RSA Key Construction
Alright, let’s see all of these RSA stuff.
In short, the generate_rsa_key_from_lcg uses LCG to find 8 256-bit primes, it then computes the RSA modulus , totient , public exponent , and finally build a public key .
def generate_rsa_key_from_lcg(self):
print('[RSA] Generating RSA key from on-chain LCG primes...')
lcg_for_rsa = LCGOracle(self.lcg_oracle.multiplier,
self.lcg_oracle.increment, self.lcg_oracle.modulus, self.seed_hash)
lcg_for_rsa.deploy_lcg_contract()
primes_arr = []
rsa_msg_count = 0
iteration_limit = 10000
iterations = 0
if len(primes_arr) < 8 and iterations < iteration_limit:
candidate = lcg_for_rsa.get_next(rsa_msg_count)
rsa_msg_count += 1
iterations += 1
if candidate.bit_length() == 256 and isPrime(candidate):
primes_arr.append(candidate)
print(f'''[RSA] - Found 256-bit prime #{len(primes_arr)}''')
if len(primes_arr) < 8 and iterations < iteration_limit:
continue
print('Primes Array: ', primes_arr)
if len(primes_arr) < 8:
error_msg = '[RSA] Error: Could not find 8 primes within iteration limit.'
print('Current Primes: ', primes_arr)
print(error_msg)
return error_msg
n = None
for p_val in primes_arr:
n *= p_val
phi = 1
for p_val in primes_arr:
phi *= p_val - 1
e = 65537
if math.gcd(e, phi) != 1:
error_msg = '[RSA] Error: Public exponent e is not coprime with phi(n). Cannot generate key.'
print(error_msg)
return error_msg
self.rsa_key = None.construct((n, e))And then all of the encryptions happen inside process_message. I can’t find where the generate_rsa_key_from_lcg method is called since my decompilation is kinda incomplete, but I’m too lazy to analyze the original Python bytecode so I’m going to guess that it’ll be called somewhere before the calls to process_message.
def process_message(self, plaintext):
if self.conversation_start_time == 0:
self.conversation_start_time = time.time()
conversation_time = int(time.time() - self.conversation_start_time)
if self.super_safe_mode and self.rsa_key:
plaintext_bytes = plaintext.encode('utf-8')
plaintext_enc = bytes_to_long(plaintext_bytes)
_enc = pow(plaintext_enc, self.rsa_key.e, self.rsa_key.n)
ciphertext = _enc.to_bytes(
self.rsa_key.n.bit_length(), 'little').rstrip(b'\x00')
encryption_mode = 'RSA'
plaintext = '[ENCRYPTED]'
else:
prime_from_lcg = self.lcg_oracle.get_next(self.message_count)
ciphertext = self.xor_oracle.encrypt(
prime_from_lcg, conversation_time, plaintext)
encryption_mode = 'LCG-XOR'
log_entry = {
'conversation_time': conversation_time,
'mode': encryption_mode,
'plaintext': plaintext,
'ciphertext': ciphertext.hex()}
self.chat_history.append(log_entry)
self.save_chat_log()
return (f'''[{conversation_time}s] {plaintext}''', f'''[{conversation_time}s] {ciphertext.hex()}''')An interesting thing is that, the LCG contract is redeployed using the exact same parameters from the initialization of the backend. Wait, if we can somehow recover the parameters of LCGOracle, can we just use them to generate the private key and break RSA?
Solving Time
At this point, I think the solution to the challenge is pretty clear.
Since we already have the first 7 messages with their plaintext, ciphertext, and conversation_time, we can recover the primes used in LCG-XOR. Using those primes, we can determine the LCG parameters (a, c, m) and the seed, then advance the generator from the seed to obtain the first eight 256-bit prime candidates. From there, reimplement the key construction logic in generate_rsa_key_from_lcg and compute the private key exponent based on ! Then we should be able to decrypt the messages with !
This is just a matter of some scripting, so let’s go ahead!
Reversing the LCG-XOR
This is actually super simple. From the analysis above, we can just do prime = ciphertext XOR plaintext XOR conversation_time to get the primes for messages 0 to 6.
In the Python script below, the first seven entries from chat_log.json are added to the log array. The plaintext is padded to 32 bytes, conversation_time is converted to a 32-byte big-endian integer, and prime is also converted to a 32-byte big-endian format.
log = [
{ "conversation_time": 0, "mode": "LCG-XOR", "plaintext": "Hello", "ciphertext": "e934b27119f12318fe16e8cd1c1678fd3b0a752eca163a7261a7e2510184bbe9" },
{ "conversation_time": 4, "mode": "LCG-XOR", "plaintext": "How are you?", "ciphertext": "25bf2fd1198392f4935dcace7d747c1e0715865b21358418e67f94163513eae4" },
{ "conversation_time": 11, "mode": "LCG-XOR", "plaintext": "Terrible...", "ciphertext": "c9f20e5561acf172305cf8f04c13e643c988aa5ab29b5499c93df112687c8c7c" },
{ "conversation_time": 13, "mode": "LCG-XOR", "plaintext": "Is this a secure channel?", "ciphertext": "3ab9c9f38e4f767a13b12569cdbf13db6bbb939e4c8a57287fb0c9def0288e46" },
{ "conversation_time": 16, "mode": "LCG-XOR", "plaintext": "Yes, it's on the blockchain.", "ciphertext": "3f6de0c2063d3e8e875737046fef079d73cc9b1b7a4b7b94da2d2867493f6fc5" },
{ "conversation_time": 24, "mode": "LCG-XOR", "plaintext": "Erm enable super safe mode", "ciphertext": "787cf6c0be39caa21b7908fcd1beca68031b7d11130005ba361c5d361b106b6d" },
{ "conversation_time": 30, "mode": "LCG-XOR", "plaintext": "Ok, activating now", "ciphertext": "632ab61849140655e0ee6f90ab00b879a3a3da241d4b50bab99f74f169d456db" },
]
p_list = []
for entry in log:
plaintext = entry["plaintext"]
conversation_time = entry["conversation_time"]
ciphertext = entry["ciphertext"]
plaintext_bytes = plaintext.encode('utf-8').ljust(32, b'\x00')
time_bytes = conversation_time.to_bytes(32, 'big')
cipher_bytes = bytes.fromhex(ciphertext)
prime_bytes = bytes(a ^ b ^ c for a, b, c in zip(
cipher_bytes, plaintext_bytes, time_bytes))
p = int.from_bytes(prime_bytes, 'big')
p_list.append(p)
print(p_list)And we can finally get these large numbers:
[
72967016216206426977511399018380411256993151454761051136963936354667101207529,
49670218548812619526153633222605091541916798863041459174610474909967699929824,
71280768003266775309606950462778030896956536610993788270598595159221463714935,
52374492464889938543708223275193226150102478572181009159069287723157087096395,
46151066309228226342793435233510111804521449597151473094879900544455543844821,
27616895455297410644582736481740143600211650471053558274523739523026009484149,
20017674779830364175685710279350076931283727675441675047445679766035806574277
]Uhh weird, some of them aren’t even prime numbers!
Well I spent some time looking back at the LCG-XOR encryption part in process_message. It turns out that these numbers don’t actually need to be prime as the encryption just uses the generated value as is without checking for primality!
prime_from_lcg = self.lcg_oracle.get_next(self.message_count)
ciphertext = self.xor_oracle.encrypt(prime_from_lcg, conversation_time, plaintext)
encryption_mode = 'LCG-XOR'So we’ve got the LCG-XOR primes. Let’s recover the parameters from here.
Recovering LCG Parameters
With these 7 numbers, how can we crack the LCG? Grok comes in handy once again and gave me this script:
from math import gcd
import sympy.ntheory as nt
s = [72967016216206426977511399018380411256993151454761051136963936354667101207529, 49670218548812619526153633222605091541916798863041459174610474909967699929824, 71280768003266775309606950462778030896956536610993788270598595159221463714935, 52374492464889938543708223275193226150102478572181009159069287723157087096395, 46151066309228226342793435233510111804521449597151473094879900544455543844821, 27616895455297410644582736481740143600211650471053558274523739523026009484149, 20017674779830364175685710279350076931283727675441675047445679766035806574277]
t = []
for i in range(1, len(s)-2):
d0 = s[i] - s[i-1]
d1 = s[i+1] - s[i]
d2 = s[i+2] - s[i+1]
ti = abs(d1**2 - d2 * d0)
t.append(ti)
m = t[0]
for ti in t[1:]:
m = gcd(m, ti)
print("m:", m)
d0 = s[1] - s[0]
d1 = s[2] - s[1]
a = (d1 * pow(d0, -1, m)) % m
print("a:", a)
c = (s[1] - a * s[0]) % m
print("c:", c)
seed = (s[0] - c) * pow(a, -1, m) % m
print("seed_hash:", seed)Here’s the parameters of the LCG after running the script:
m: 98931271253110664660254761255117471820360598758511684442313187065390755933409
a: 11352347617227399966276728996677942514782456048827240690093985172111341259890
c: 61077733451871028544335625522563534065222147972493076369037987394712960199707
seed_hash: 80631529052001100272845413254760303954872303349693249834992925889079643767931While I was doing research on this, I came across this blog post which demonstrates the same cracking approach as Grok’s. It’s worth checking out btw.
Cracking RSA
We’re going to use the exact logic to generate the RSA key as in generate_rsa_key_from_lcg. Another thing to do is to calculate the private key exponent as (modular inverse of e modulo phi) for decrypting the messages.
Generating RSA Primes
This part is just straight copying from the generate_rsa_key_from_lcg function:
import sympy.ntheory as nt
a = 11352347617227399966276728996677942514782456048827240690093985172111341259890
c = 61077733451871028544335625522563534065222147972493076369037987394712960199707
m = 98931271253110664660254761255117471820360598758511684442313187065390755933409
state = 80631529052001100272845413254760303954872303349693249834992925889079643767931
primes = []
counter = 0
iteration_limit = 10000
while len(primes) < 8 and counter < iteration_limit:
candidate = (a * state + c) % m
state = candidate
counter += 1
if candidate.bit_length() == 256 and nt.isprime(candidate):
primes.append(candidate)
print(primes)Running the script yielded eight 256-bit primes:
[
72967016216206426977511399018380411256993151454761051136963936354667101207529,
79611551309049018061300429096903741339200167241148430095608259960783012192237,
75395288067150543091997907493708187002382230701390674177789205231462589994993,
62826068095404038148338678434404643116583820572865189787368764098892510936793,
69802783227378026511719332106789335301376047817734407431543841272855455052067,
68446593057460676025047989394445774862028837156496043637575024036696645401289,
82836473202091099900869551647600727408082364801577205107017971703263472445197,
88790251731800173019114073860734130032527125661685690883849562991870715928701
]Decryptions, Finally!
Once again, the code for calculating phi is copied from generate_rsa_key_from_lcg, with some minor modifications. We’re going to calculate d = pow(e, -1, phi) to obtain the private key exponent.
If you look more closely at the process_message method, ciphertexts are actually little-endian bytes. To decrypt, we’ll compute msg = pow(c, d, n) where c is a ciphertext from chat_log.json, convert it to big-endian bytes, then decode the bytes as UTF-8 to obtain the unencrypted messages.
primes = [72967016216206426977511399018380411256993151454761051136963936354667101207529, 79611551309049018061300429096903741339200167241148430095608259960783012192237, 75395288067150543091997907493708187002382230701390674177789205231462589994993, 62826068095404038148338678434404643116583820572865189787368764098892510936793, 69802783227378026511719332106789335301376047817734407431543841272855455052067, 68446593057460676025047989394445774862028837156496043637575024036696645401289, 82836473202091099900869551647600727408082364801577205107017971703263472445197, 88790251731800173019114073860734130032527125661685690883849562991870715928701]
n = 1
for p in primes:
n *= p
phi = 1
for p in primes:
phi *= (p - 1)
e = 65537
d = pow(e, -1, phi)
# From chat_logs.json
rsa_ciphertexts = [
"680a65364a498aa87cf17c934ab308b2aee0014aee5b0b7d289b5108677c7ad1eb3bcfbcad7582f87cb3f242391bea7e70e8c01f3ad53ac69488713daea76bb3a524bd2a4bbbc2cfb487477e9d91783f103bd6729b15a4ae99cb93f0db22a467ce12f8d56acaef5d1652c54f495db7bc88aa423bc1c2b60a6ecaede2f4273f6dce265f6c664ec583d7bd75d2fb849d77fa11d05de891b5a706eb103b7dbdb4e5a4a2e72445b61b83fd931cae34e5eaab931037db72ba14e41a70de94472e949ca3cf2135c2ccef0e9b6fa7dd3aaf29a946d165f6ca452466168c32c43c91f159928efb3624e56430b14a0728c52f2668ab26f837120d7af36baf48192ceb3002",
"6f70034472ce115fc82a08560bd22f0e7f373e6ef27bca6e4c8f67fedf4031be23bf50311b4720fe74836b352b34c42db46341cac60298f2fa768f775a9c3da0c6705e0ce11d19b3cbdcf51309c22744e96a19576a8de0e1195f2dab21a3f1b0ef5086afcffa2e086e7738e5032cb5503df39e4bf4bdf620af7aa0f752dac942be50e7fec9a82b63f5c8faf07306e2a2e605bb93df09951c8ad46e5a2572e333484cae16be41929523c83c0d4ca317ef72ea9cde1d5630ebf6c244803d2dc1da0a1eefaafa82339bf0e6cf4bf41b1a2a90f7b2e25313a021eafa6234643acb9d5c9c22674d7bc793f1822743b48227a814a7a6604694296f33c2c59e743f4106",
]
for cipher_hex in rsa_ciphertexts:
c = int.from_bytes(bytes.fromhex(cipher_hex), 'little')
msg_int = pow(c, d, n)
msg_bytes = msg_int.to_bytes((msg_int.bit_length() + 7) // 8, 'big')
msg_str = msg_bytes.decode('utf-8')
print(msg_str)The above script prints the decrypted messages with the flag:
Actually what's your email?
It's W3b3_i5_Gr8@flare-on.comW3b3_i5_Gr8@flare-on.com Thoughts
I did try solving the challenge by tossing the decompilation and the chat log file into Grok LOL, since I heard someone said that LLMs are powerful at solving cryptography challenges. And Grok nailed this with just one shot!
In the end, I chose to actually solve this challenge myself, since it was my first Flare-On and I couldn’t get past the 7th challenge. I feels like this challenge is more about cryptography rather than reversing, but it is still super interesting and definitely taught me something about LCG and RSA!