Priority Queues and Hash Tables - DSA #8

In this note, we’ll explore two powerful data structures: Priority Queues and Hash Tables! These structures drive many popular algorithms, making them both fascinating and essential to understand.

Priority Queues

We’re all familiar with the basic concept of a Queue—a linear data structure that follows the FIFO (First-In, First-Out) principle, meaning the first element inserted is the first to be removed. However, Priority Queues operate differently despite their similar name. But why do we need them?

Imagine you need to develop software to manage a hospital's emergency room. The software must track patients and determine the order in which they receive care. When a patient arrives, the staff creates a record in the database. What data structure would you use to store these records? 

Initially, you might consider a sorted list to treat patients alphabetically by name. However, it's not fair to prioritize a patient with a minor issue (e.g., “Donald” with a splinter) over a patient with a critical condition (e.g., “Mickey” with a high fever). A simple queue based on the order of arrival is also unsuitable. 

Emergency room staff assign an urgency or priority level to patients. The patient with the highest priority is treated by the next available doctor. Therefore, we need a data structure that can efficiently provide the patient with the highest priority. A Priority Queue is the appropriate data structure for this scenario. 

Basic Concept of Priority Queues

A Priority Queue is a data structure for maintaining a set of elements, each with an associated value called a priority.

A priority value indicates a task’s priority for completion.

In the above scenario, the priority value indicates a patient’s priority for treatment.

A priority value of natural numbers ($\in ℕ$) should be good enough in most cases. There are two ways for the value to indicate the priority, including smallest to highest for increasing priority, and vice-versa. In this note, we’ll assume that the smallest priority value indicates the highest priority.

Priority Queue Operations

The Queue data structure provides three operations:

• isEmpty for checking whether a priority queue is empty.
• enQueue for inserting a new element into the queue.
• deQueue for removing and returning the element at the beginning of the queue.

A Priority Queue has equivalent operations, often referred to as Test, Insertion, and Extraction. Additionally, it supports two more operations:

• Get: for getting the element in the priority queue with the highest priority.
• Update: update the $i^{th}$ element’s priority value with the new value.

In this note, we’ll be focusing on the Test, Insertion, and Extraction operations.

Implementation of Priority Queues

Using Singly-Linked List or Array

A singly-linked list is a relatively simple way to implement a priority queue. You can create a new list and insert new elements at the beginning.

Here's a singly-linked list definition for implementing a Priority Queue:

typedef struct Node* Ref;
struct Node {
	int pV; // The priority value
	Node* next;
};

Since we're arranging elements based on priority, should we use a sorted singly-linked list? Let's start with an unsorted list.

Using Unsorted Singly-Linked List

Let’s implement the function Test to check if a priority queue is empty. The Test function has a time complexity of $\Theta(1)$.

Test(Ref pQ) {
	return (pQ == NULL);
}

For the insertion operation, we insert a new node at the beginning of the priority queue.

Insertion(Ref &pQ, Ref p) {
	p->next = pQ;
	pQ = p;
}

For the Extraction operation, we need to identify and remove the element with the highest priority. This requires $\mathcal{O}(n)$ time. However, this operation should be as fast as possible. Therefore, an unsorted singly-linked list is not ideal.

Using Sorted Singly-Linked List

This singly-linked list is going to be arranged in ascending order of the elements based on their priority.

The Test function is simply just check if the first element reference of the priority queue is NULL, basically the same as the one that we’ve done previously.

Since we’re using a sorted singly-linked list, the first node of the list is the one with the smallest priority value. By extracting the first element, we can get the element whose priority is the highest. This can be done in $\Theta(1)$ time.

Extraction(Ref &pQ) {
	if (!pQ) return;
	Ref p = pQ;
	p = pQ->next;
	p->next = NULL;
	return p;
}

For the Insertion function, there’s actually a great technique to insert a new node into a sorted singly-linked list demonstrated by Niklaus Wirth in his book Algorithms + Data Structures = Programs. It’s actually utilizing two different pointers running in parallel. This is how this works:

This is our sorted singly-linked list priority queue…

…and the node that we’re going to insert into the linked list.

We’ll define two pointers, p2 which points to the first element of our linked list, and p1 which points to the next element of the first one. We’re going to refer p1 as the “current” node while traversing the linked list.

Now, we keep traversing through the list while we hasn’t reached the tail (p1 ≠ NULL) and the priority value of the “current” node is smaller than that of the node to be inserted (p1->pV < p->pV).

When we reach the node where its priority value is larger or equal to the one to be inserted, stop traversing though the linked list. At this point, we insert the new node between the previous node p2 and the “current” node p1 by updating the pointers: p2->next = p links the previous node to the new node, and p->next = p1 connects the new node to the “current” node.

Insertion(Ref &pQ, Ref p) {
	Ref p2 = pQ, p1 = pQ->next;
	while (p1 && p1->pV < p->pV) {
		p2 = p1; p1 = p1->next;
	}
	p2->next = p; p->next = p1;
}

What happens if the priority queue is empty? In that case, pQ->next doesn't exist. To handle this, we can use a dummy head node for our linked list, which doesn't store data. This allows us to call the Insertion operation without errors.

Ref pQ = new Node;
pQ->next = NULL;
Insertion(pQ, p);

Using Min-Heap

In reality, we use a min-heap for implementing the Priority Queue data structure. In a min-heap, the smallest element is always at the top (the root).

The Extraction operation involves retrieving and removing this minimum element. For the Insertion operation, we can use the same approach as in Heap Sort in Advanced Sorting Algorithms - DSA #6: place the new element at the end of the array and swap it with the first element. After both operations, we must reconstruct the heap using the sifting algorithm to maintain its structure. 

Since we use the sifting algorithm, both operations have a time complexity of $\mathcal{O}(\log n)$.

Using Balanced Binary Search Tree

This implementation of the Priority Queue using Balanced Binary Search Tree will be introduced in a future note. However, this implementation isn’t efficient in practice. More information can be found in the source below.

Implementing priority queue using max heap vs balanced BST

Balanced BST and max heap both perform insert and delete in O(logn). However, finding max value in a max heap is O(1) but this is O(logn) in balanced BST. If we remove the max value in a max heap it

https://stackoverflow.com/questions/65882138/implementing-priority-queue-using-max-heap-vs-balanced-bst

Hash Tables

Introduction to Hash Tables

In computing, the most common operations on a set of elements include searching for a specific element, inserting a new element, and deleting an existing element. A data structure that supports these three operations is called a dictionary. There are quite a few ways a dictionary can be implemented, and one of them is the hashing technique.

Hashing

Firstly, let’s assume that we have to implement a dictionary of $n$ records with keys $k_1, k_2, \dots, k_n$.

Hashing is based on the idea of distributing keys among a one-dimensional array $H[0..m - 1]$ called a Hash Table. Given a predefined function $h$ (called hash function), the distribution is done by computing the value $h(k_i), \forall i \in [1,n]$. To be more specific, $h(k_i) \in [0, m - 1]$ is called a hash value and determines the location where the key is stored in the hash table.

Hash Function

There are a lot of simple hash functions, and each can be used for different types of keys, including integers, letters, and character strings.

• If the keys are non-negative integers, a simple hash function can be defined as:
  $h(k) = k \mod m$

  where $k$ is the key, $m$ is the size of the hash table, and $mod$ denotes the modulus operator. For example, if $k = 37$ and $m = 10$, then $h(37) = 37 \mod 10 = 7$.

• If the keys are letters from some alphabet $\Sigma$, we need to first convert them into numerical values. A simple approach is to use their ordinal value, or their position in the alphabet:
  $h(k) = \text{ord}(k) \mod m$

  where $\text{ord}(k)$ gives the position of the letter in the alphabet, and $m$ is the table size. For example, if $k = D$, and assuming $\text{ord}(D) = 4$, then $h(D) = 4 \mod 10 = 4$.

• When keys are strings (e.g., words), we extend our approach by summing the ordinal values of each character and then applying the modulus operation:
  $h(k) = \left( \sum_{i=1}^{n} \text{ord}(c_i) \right) \mod m$

  where $c_i$ is the $i^{th}$ character of the string, $\text{ord}(c_i)$ is the ordinal value of character $c_i$, $n$ is the length of the string, and $m$ is the hash table size. For example, if $k = \text{“CAT”}$ and using $\text{ord}(C) = 3$, $\text{ord}(A) = 1$, $\text{ord}(T) = 20$, $h(\text{“CAT”}) = (3+1+20) \mod 10 = 24 \mod 10 = 4$.

Let’s see the hash function in action! We’ll use the most basic hash function $h(k) = k \mod m$ for demonstration purpose.

In general, a hash function needs to satisfy some requirements. It should evenly distribute keys across the hash table, be computationally efficient, and operate in constant time, regardless of the number of keys or the table’s size.

Collisions

Collision is a phenomenon of two (or more) keys being hashed into the same cell of the hash table.

If the hash table size $m$ is smaller than the number of keys $n$, collisions are inevitable. Even when $m$ is significantly larger than $n$, collisions can still occur. However, with a well-chosen table size and an effective hash function, collisions become rare.

Every hashing scheme requires a collision resolution mechanism, which differs between the two primary types of hashing:

• Open Hashing (or Separate Chaining)
• Closed Hashing (or Open Addressing)

Open Hashing (Separate Chaining)

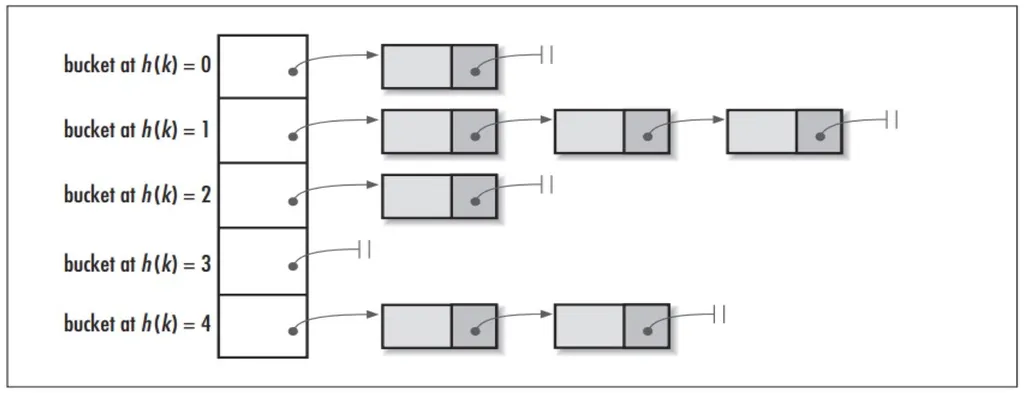
In open hashing, the keys are stored on linked lists (or buckets) attached to cells of the hash table. Each bucket contains all the keys hashed to its cell.

We will use these definitions for the pseudo-code implementations:

typedef struct HashNode* Ref;
struct HashNode {
	string key;
	int value;
	HashNode* next;
};

Ref table[1..m]

Search Operation of Open Hashing

To search for a key $k$ in the hash table, we first compute its hash value $h(k)$, using a hash function.

If the bucket at index $h(k)$ is empty, the key is not present in the table. However, if the bucket is occupied, it may contain $k$ or other keys that have hashed to the same index due to collisions. In such cases, we traverse the bucket to check for an occurrence of $k$, ensuring that the correct key is found.

Search(key) {
	index = hashFunction(key);
	Ref p = table[index];
	
	// Traverse the bucket
	while (p) { 
		if (p->key == key) return p;
		p = p->next;
	}
	
	return NULL;
}

Insertion Operation of Open Hashing

To insert a key $k$ into a hash table, we first check whether it is already present. This involves computing its hash value $h(k)$ and searching the corresponding bucket.

If the key is found, no further action is needed. If the search is unsuccessful, meaning $k$ is not yet in the table, it is added to the bucket at index $h(k)$.

Insertion(key, value) {
	index = hashFunction(key);
	
	// Do nothing if the key is already present
	if (Search(key)) return;
	
	// Add the key to the beginning of the bucket
	Ref p = new HashNode{ key, value, table[index] };
	table[index] = p;
}

Deletion Operation of Open Hashing

To remove a key $k$ in the hash table, we first search for it by computing its hash value $h(k)$ and checking the corresponding bucket. If the key is found, the node containing $k$ is deleted from the bucket at index $h(k)$. If the key is not found, no action is needed, as it is not present in the table.

Deletion(key) {
	index = hashFunction(key);
	
	// Bucket is empty -> Key does not exist
	if (!table[index]) return;
	
	// Key is found at the head of the linked list
	if (table[index]->key == key) {
		// Delete the head
		Ref p = table[index];
		table[index] = table[index]->next;
		delete p;
		return;
	} 
	
	// Use two pointers to traverse the linked list
	// Similar to the Insertion operation of Priority Queue
	Ref p2 = table[index], p1 = table[index]->next;
	while (p1 && p1->key != key) {
		p2 = p1; p1 = p1->next;
	}
	
	// If found, delete the node containing the key
	if (!p1) return;
	p2->next = p1->next;
	delete p1;
}

Analysis of Open Hashing

The efficiency of Open Hashing depends on the lengths of the buckets, which, in turn, depend on the table size and the quality of the hash function.

If $n$ keys are distributed among $m$ cells of the hash table evenly, the length of each bucket will be about $\alpha = \frac{n}{m}$, where $\alpha$ is called the load factor of the hash table and should not be far from $1$.

• $\alpha \ll 1$ indicates an efficient use of space, as there are too many empty singly-linked list in the hash table.
• $\alpha \gg 1$ indicates that the linked lists are very long, which will take more time to perform operations on these lists.
• $\alpha \approx 1$ is our preferred load factor, most of the time we only need one comparison (or constant time) to perform the three operations on the hash table.

Closed Hashing (Open Addressing)

In closed hashing, all keys are stored in the hash table itself without the use of linked lists. Therefore, the table size $m$ must be at least as large as the number of records $n$.

There are different strategies that can be employed for collision resolution, with the simplest one being called linear probing. The idea of this strategy is to check the cell located next to the position where collision occurs.

We will use these definitions for the implementation of the hash table:

struct HashNode {
	string key;
	int value;
}

HashNode* table[1..m]

Search Operation of Closed Hashing

To search for a key $k$ in a hash table, its hash value $h(k)$ is first computed.

If the cell at index $h(k)$ is empty, the search is unsuccessful.

This process repeats until either a matching key is found or an empty cell is encountered, indicating an unsuccessful search. If the end of the hash table is reached, the search wraps around to the beginning of the table. In other words, the hash table is now a circular array!

Search(key) {
	hashValue = hashFunction(key);
	
	// The 'for' loop for probing
	for (i = 0; i < m; i++) {
		// Calculate the index of the cell
		index = (hashValue + i) % m;
		
		if (!table[index]) 
			return NULL;
		if (table[index]->key == key) 
			return table[index];
	}
	return NULL;
}

Insertion Operation of Closed Hashing

To insert a key $k$ into a hash table, the process begins by searching for an empty cell. This involves computing the hash value $h(k)$ and checking if the corresponding index is available. If the cell is occupied, the search continues by checking the next cell, until an empty cell is found. Once located, $k$ is inserted into the empty cell.

Insertion(key, value) {
	hashValue = hashFunction(key);
	
	for (i = 0; i < m; i++) {
		index = (hashValue + i) % m;
		
		if (!table[index]) { 
			// Insert into the empty cell
			table[index] = new hashNode{ key, value };
			return;
		} else if (table[index]->key == key) {
			// The key already exists --> Update its key value
			table[index]->value = value;
			return;
		}
	}
}

Rehashing

If the hash table is full, operations like the Insertion operation will fail.

Rehashing is a process used to handle situations where a hash table becomes full or nearly full. When rehashing occurs, the current hash table is scanned, and all its key are relocated into a larger table.

Deletion Operation of Closed Hashing

To remove a key $k$, we first search for it in within the hash table by computing the hash value $h(k)$. If the search is successful, $k$ is deleted from the cell.

However, a challenge arises when $k$ is in the table, but the search is unsuccessful due to the probing method used! This issue occurs because deletion can disrupt the search chain, leading to failed lookups for existing keys!

To handle this, previously occupied locations should be marked with a special symbol to distinguish them from locations that have not been occupied!

Deletion(key) {
	hashValue = hashFunction(key);
	for (i = 0; i < m; i++) {
		index = (hashValue + i) % m;
		if (!table[index]) return;
		if (table[index] != -∞ && table[index]->key == key) {
			// Mark the cell as deleted with -∞
			table[index] = -∞
			return;
		}
	}
}

Since we’re marking deleted keys with $-∞$, we will also need to modify the Search and Insertion function to treat the cells with $-∞$ as empty cells.

// For the 'Search' function
if (!table[index] || table[index] == -∞) 
	return NULL; // .... and the rest of the function
		
		
// For the 'Insertion' function
if (!table[index] || table[index] == -∞) { 
	table[index] = new hashNode{ key, value };
	return;
} else { // .... and the rest of the function

Analysis of Closed Hashing

Analyzing linear probing is much harder than open hashing because collisions can cause clusters of occupied cells, slowing things down. When the table isn’t too full, operations usually take about one cell access on average.

👏 Thanks for reading!